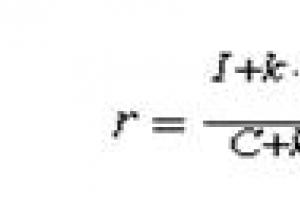Tentin tehtävien tehtävien laajuus. Tyypillisten ongelmien ratkaiseminen Etsi 4 x 2 -funktion arvojoukko
Monet tehtävät saavat meidät etsimään funktioarvoja tietyltä segmentiltä tai koko määritelmäalueelta. Tällaisia tehtäviä ovat erilaiset lausekkeiden arvioinnit, eriarvoisuuksien ratkaiseminen.
Tässä artikkelissa määrittelemme funktion alueen, harkitsemme menetelmiä sen löytämiseksi ja analysoimme yksityiskohtaisesti esimerkkien ratkaisua yksinkertaisista monimutkaisempiin. Kaikki materiaali on varustettu graafisilla kuvilla selvyyden vuoksi. Joten tämä artikkeli on yksityiskohtainen vastaus kysymykseen, kuinka löytää funktion alue.
Määritelmä.
Funktion y = f(x) arvot välissä X kutsutaan funktion kaikkien arvojen joukoksi, jonka se ottaa, kun iteroidaan kaikkialla.
Määritelmä.
Funktio y = f(x) kutsutaan funktion kaikkien arvojen joukoksi, jonka se ottaa, kun iteroidaan kaikkia x määrittelyalueelta.
Funktioalue on merkitty E(f) .
Funktion alue ja funktion arvojoukko eivät ole sama asia. Näitä käsitteitä pidetään vastaavina, jos väli X, kun löydetään funktion y = f(x) arvojoukko, osuu yhteen funktion toimialueen kanssa.
Älä myöskään sekoita funktion aluetta yhtälön y=f(x) oikealla puolella olevan lausekkeen muuttujaan x. Muuttujan x sallittujen arvojen alue lausekkeelle f(x) on funktion y=f(x) määritelmän alue.
Kuvassa on muutamia esimerkkejä.
Funktiokaaviot on esitetty lihavoituin sinisin viivoin, ohuet punaiset viivat ovat asymptootteja, punaiset pisteet ja viivat Oy-akselilla osoittavat vastaavan funktion alueen.
Kuten näet, funktion alue saadaan projisoimalla funktion kuvaaja y-akselille. Se voi olla yksittäinen luku (ensimmäinen tapaus), numerosarja (toinen tapaus), segmentti (kolmas tapaus), intervalli (neljäs tapaus), avoin säde (viides tapaus), liitto (kuudes tapaus) jne. .
Joten mitä sinun on tehtävä löytääksesi funktion alueen.
Aloitetaan yksinkertaisimmasta tapauksesta: näytämme, kuinka määritetään jatkuvan funktion y = f(x) arvot välissä .
Tiedetään, että segmentillä jatkuva funktio saavuttaa maksimi- ja minimiarvonsa siinä. Siten segmentin alkuperäisen funktion arvojen joukko on segmentti 
. Siksi tehtävämme rajoittuu funktion suurimman ja pienimmän arvojen löytämiseen väliltä .
Etsitään esimerkiksi arcsinifunktion alue.
Esimerkki.
Määritä funktion y = arcsinx alue.
Ratkaisu.
Arsinin määritelmäalue on segmentti [-1; 1] . Etsi tämän segmentin funktion suurin ja pienin arvo. 
Derivaata on positiivinen kaikille x:ille väliltä (-1; 1) , eli arsinifunktio kasvaa koko määritelmäalueen yli. Siksi se ottaa pienimmän arvon, kun x = -1, ja suurimman, kun x = 1. 
Saimme arcsinifunktion alueen 
.
Esimerkki.
Etsi funktioarvojen joukko 
segmentillä.
Ratkaisu.
Etsi funktion suurin ja pienin arvo annetusta segmentistä.
Määritellään segmenttiin kuuluvat ääripisteet: 
Laskemme alkuperäisen funktion arvot janan päissä ja pisteissä 
:
Siksi segmentin funktion arvojen joukko on segmentti 
.
Nyt näytämme kuinka löytää jatkuvan funktion y = f(x) arvojen joukko väliltä (a; b) , .
Ensin määritetään funktion ääripisteet, funktion ääriarvot, funktion kasvu- ja laskuvälit tietyllä aikavälillä. Seuraavaksi lasketaan intervallin päissä ja (tai) rajat äärettömyydessä (eli tutkitaan funktion käyttäytymistä intervallin rajoilla tai äärettömässä). Nämä tiedot riittävät funktioarvojen joukon löytämiseen tällaisilla aikaväleillä.
Esimerkki.
Määritä funktioarvojen joukko väliltä (-2; 2) .
Ratkaisu.
Etsitään välille (-2; 2) osuvat funktion ääripisteet: 
Piste x = 0 on maksimipiste, koska derivaatta muuttaa etumerkkiä plussasta miinukseen kulkiessaan sen läpi ja funktion kuvaaja siirtyy kasvavasta laskevaan. 
on funktion vastaava maksimi.
Selvitetään funktion käyttäytyminen, kun x pyrkii -2:een oikealla ja kun x pyrkii 2:een vasemmalla, eli löydämme yksipuoliset rajat: 
Mitä saimme: kun argumentti muuttuu arvosta -2 nollaan, funktion arvot kasvavat miinus äärettömyydestä miinus neljäsosaan (funktion maksimi kohdassa x = 0 ), kun argumentti muuttuu nollasta 2:ksi, funktio arvot pienenevät miinus äärettömään. Siten välin (-2; 2) funktioarvojen joukko on .
Esimerkki.
Määritä välin tangenttifunktion y = tgx arvot.
Ratkaisu.
Välin tangenttifunktion derivaatta on positiivinen 
, mikä tarkoittaa toiminnon lisääntymistä. Tutkimme funktion käyttäytymistä intervallin rajoilla: 
Näin ollen, kun argumentti muuttuu arvosta arvoon, funktion arvot kasvavat miinus äärettömästä plus äärettömään, eli tangenttiarvojen joukko tällä välillä on kaikkien reaalilukujen joukko.
Esimerkki.
Etsi luonnollisen logaritmifunktion alue y = lnx .
Ratkaisu.
Luonnollinen logaritmifunktio määritellään argumentin positiivisille arvoille 
. Tällä aikavälillä derivaatta on positiivinen 
, tämä osoittaa sen toiminnon lisääntymistä. Etsitään funktion yksipuolinen raja, koska argumentti pyrkii nollaan oikealta ja raja x:llä plus äärettömään: 
Näemme, että kun x muuttuu nollasta plus äärettömään, funktion arvot kasvavat miinus äärettömästä plus äärettömään. Siksi luonnollisen logaritmifunktion alue on koko reaalilukujen joukko.
Esimerkki.
Ratkaisu.
Tämä funktio on määritetty kaikille todellisille x-arvoille. Määritetään funktion ääripisteet sekä kasvu- ja laskuvälit. 
Siksi funktio pienenee kohdassa , kasvaa kohdassa , x = 0 on maksimipiste, 
funktion vastaava maksimi.
Katsotaanpa funktion käyttäytymistä äärettömässä: 
Siten äärettömyydessä funktion arvot lähestyvät asymptoottisesti nollaa.
Huomasimme, että kun argumentti muuttuu miinus äärettömästä nollaan (maksimipiste), funktion arvot kasvavat nollasta yhdeksään (funktion maksimiarvoon asti), ja kun x muuttuu nollasta plus äärettömään, funktion arvot pienenevät yhdeksästä nollaan.
Katso kaaviokuvaa.
Nyt on selvästi nähtävissä, että funktion alue on .
Funktion y = f(x) arvojen joukon löytäminen intervalleilta vaatii samanlaisia tutkimuksia. Emme nyt käsittele näitä tapauksia yksityiskohtaisesti. Näemme ne alla olevissa esimerkeissä.
Olkoon funktion y = f(x) alue useiden intervallien liitto. Kun löydetään tällaisen funktion alue, määritetään kunkin intervallin arvojoukot ja otetaan niiden liitto.
Esimerkki.
Etsi funktion alue.
Ratkaisu.
Funktiomme nimittäjä ei saa mennä nollaan, eli .
Etsitään ensin funktion arvojoukko avoimelta säteeltä.
Funktiojohdannainen 
on negatiivinen tällä välillä, eli funktio pienenee sillä. 
Huomasimme, että koska argumentti pyrkii miinus äärettömään, funktion arvot lähestyvät asymptoottisesti yksikköä. Kun x muuttuu miinus äärettömästä kahteen, funktion arvot laskevat yhdestä miinus äärettömyyteen, eli tarkasteluvälillä funktio saa joukon arvoja. Emme sisällytä yhtenäisyyttä, koska funktion arvot eivät saavuta sitä, vaan vain asymptoottisesti pyrkivät siihen miinus äärettömyydessä.
Toimimme samalla tavalla avoimen säteen kohdalla.
Toiminto pienenee myös tällä aikavälillä. 
Tämän intervallin funktioarvojen joukko on joukko .
Siten haluttu funktioarvojen alue on joukkojen liitto ja .
Graafinen kuva.
Erikseen meidän tulisi keskittyä jaksollisiin funktioihin. Jaksollisten funktioiden alue on sama kuin tämän funktion jaksoa vastaavan aikavälin arvot.
Esimerkki.
Etsi sinifunktion y = sinx alue.
Ratkaisu.
Tämä funktio on jaksollinen kahden pi:n jaksolla. Otetaan segmentti ja määritetään sille arvojoukko. 
Segmentti sisältää kaksi ääriarvopistettä ja .
Laskemme funktion arvot näissä pisteissä ja segmentin rajoilla, valitsemme pienimmät ja suurimmat arvot: 
Siten, 
.
Esimerkki.
Etsi funktion alue 
.
Ratkaisu.
Tiedämme, että arkosiinin alue on segmentti nollasta pi:hen, eli 
tai toisessa postauksessa. Toiminto 
voidaan saada arccosxista siirtämällä ja venyttämällä x-akselia pitkin. Tällaiset muunnokset eivät vaikuta alueeseen, joten 
. Toiminto 
tulee venytetään kolme kertaa Oy-akselia pitkin, eli 
. Ja muunnosten viimeinen vaihe on siirtymä neljällä yksiköllä alaspäin y-akselia pitkin. Tämä johtaa meidät kaksinkertaiseen eriarvoisuuteen 
Siten haluttu arvoalue on 
.
Annetaan ratkaisu toiseen esimerkkiin, mutta ilman selityksiä (niitä ei vaadita, koska ne ovat täysin samanlaisia).
Esimerkki.
Määritä toimintoalue 
.
Ratkaisu.
Kirjoitamme alkuperäisen funktion muotoon 
. Eksponentiaalisen funktion alue on väli . Tuo on, . Sitten 
Siten, 
.
Kuvan täydentämiseksi meidän pitäisi puhua sellaisen funktion alueen löytämisestä, joka ei ole jatkuva määritelmäalueella. Tässä tapauksessa määritelmäalue jaetaan katkaisupisteillä intervalleiksi, ja löydämme arvojoukot jokaisesta niistä. Yhdistämällä saadut arvojoukot saadaan alkuperäisen funktion arvoalue. Suosittelemme muistamaan 3 vasemmalla, funktion arvot yleensä miinus yksi, ja kun x yleensä 3 oikealla, funktion arvot yleensä plus ääretön.
Siten funktion määrittelyalue on jaettu kolmeen väliin.
Välillä meillä on funktio 
. Siitä lähtien 
Näin ollen alkuperäisen funktion arvojen joukko välissä on [-6;2] .
Puolivälillä meillä on vakiofunktio y = -1 . Eli alkuperäisen funktion arvojoukko intervallilla koostuu yhdestä elementistä .
Funktio on määritetty kaikille argumentin kelvollisille arvoille. Selvitä funktion kasvu- ja laskuvälit.
Derivaata katoaa kohdissa x=-1 ja x=3 . Merkitsemme nämä pisteet reaaliakselille ja määritämme derivaatan merkit saaduille intervalleille. 
Toiminto pienenee 
, kasvaa [-1; 3] , x=-1 minimipiste, x=3 maksimipiste.
Laskemme vastaavat minimi- ja maksimifunktiot: 
Tarkastetaan funktion käyttäytymistä äärettömässä: 
Toinen raja laskettiin .
Tehdään kaavamainen piirustus.
Kun argumentti muuttuu miinus äärettömästä arvoon -1, funktion arvot pienenevät plus äärettömästä arvoon -2e, kun argumentti muuttuu arvosta -1 arvoon 3, funktion arvot kasvavat arvosta -2e arvoon , kun argumentti muuttuu arvosta -2e. 3 plus äärettömään, funktion arvot pienenevät nollaan, mutta ne eivät saavuta nollaa.
Toiminto on malli. Määritellään X itsenäisen muuttujan arvojoukoksi // riippumaton tarkoittaa mitä tahansa.
Funktio on sääntö, jonka mukaan jokaiselle joukon X riippumattoman muuttujan arvolle voidaan löytää riippumattoman muuttujan ainoa arvo. // eli jokaista x:ää kohti on yksi y.
Määritelmästä seuraa, että on olemassa kaksi käsitettä - riippumaton muuttuja (jonka merkitsemme x:llä ja se voi saada minkä tahansa arvon) ja riippuvainen muuttuja (jota merkitsemme y:llä tai f (x) ja se lasketaan funktiosta, kun korvaamme x).
ESIMERKKI y=5+x
1. Riippumaton on x, joten otamme minkä tahansa arvon, olkoon x = 3
2. ja nyt lasketaan y, joten y \u003d 5 + x \u003d 5 + 3 \u003d 8. (y on riippuvainen x:stä, koska minkä x:n korvaamme, saamme sellaisen y:n)
Sanotaan, että muuttuja y on toiminnallisesti riippuvainen muuttujasta x ja tätä merkitään seuraavasti: y = f (x).
ESIMERKIKSI.
1.y = 1/x. (kutsutaan hyperboliksi)
2. y=x^2. (kutsutaan paraabeliksi)
3.y=3x+7. (kutsutaan suoraksi)
4. y \u003d √ x. (kutsutaan paraabelin haaraksi)
Riippumatonta muuttujaa (jota merkitsemme x:llä) kutsutaan funktion argumentiksi.
Toiminnan laajuus
Kaikkien arvojen joukkoa, jonka funktion argumentti ottaa, kutsutaan funktion toimialueeksi, ja sitä merkitään D(f) tai D(y).
Tarkastellaan D(y) arvoa 1.,2.,3.,4.
1. D (y)= (∞; 0) ja (0;+∞) //koko joukko reaalilukuja nollaa lukuun ottamatta.
2. D (y) \u003d (∞; +∞) / / kaikki monet reaaliluvut
3. D (y) \u003d (∞; +∞) / / kaikki monet reaaliluvut
4. D (y) \u003d
Esimerkkejä
Etsi funktioarvojen joukko:
Käyttäen johdannaista
Etsi määritelmän alue: D(f)=[-3;3], koska $9-x^(2)\geq 0$
Etsi derivaatta: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$
f"(x) = 0, jos x = 0. f"(x) ei ole olemassa, jos $\sqrt(9-x^(2))=0$ eli x = ±3. Saamme kolme kriittistä pistettä: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, joista kaksi osuu segmentin päihin. Laske: f(–3) = 0, f(0) = 3, f(3) = 0. Näin ollen f(x):n pienin arvo on 0, suurin arvo on 3.
Vastaus: E(f) = .
EI käytä johdannaista
Etsi funktion suurin ja pienin arvo:
$ lähtien
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , sitten:
$f(x)\leq \frac(3)(4)$ kaikille x;
$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ kaikille x(koska $|\cos (x)|\leq 1$);
$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;
$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;
Vastaus: $\frac(3)(4)$ ja $-\frac(3)(2)$
Jos ratkaiset tämän ongelman johdannaisten avulla, sinun on voitettava esteet, jotka liittyvät siihen, että funktio f (x) ei ole määritelty segmentissä, vaan koko todellisessa suorassa.
Rajat/arviot -menetelmää käyttämällä
Sinin määritelmästä seuraa, että $-1\leq\sin(x)\leq 1$. Seuraavaksi käytämme numeeristen epäyhtälöiden ominaisuuksia.
$-4\leq - 4\sin(x)\leq 4$, (kerrotaan kaikki kolme kaksois-epäyhtälön osaa -4:llä);
$1\leq 5 - 4\sin(x)\leq 9$ (lisätty kaksinkertaisen epäyhtälön 5 kolmeen osaan);
Koska annettu toiminto on jatkuva koko määritelmäalueella, silloin sen arvojen joukko on sen pienimmän ja suurimman arvojen välissä koko määritelmäalueella, jos sellainen on.
Tässä tapauksessa funktion $y = 5 - 4\sin(x)$ arvojoukko on joukko .
Epäyhtälöistä $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ saadaan arvio $$\\ -6\leq y\ leq 6 $ $
Kun x = p ja x = 0, funktio saa arvot -6 ja 6, ts. saavuttaa ala- ja ylärajan. Jatkuvien funktioiden cos(7x) ja cos(x) lineaarisena yhdistelmänä funktio y on jatkuva koko lukuakselilla, joten jatkuvan funktion ominaisuuden perusteella se ottaa kaikki arvot välillä -6:sta 6:een. , ja vain ne, koska epäyhtälöiden $- 6\leq y\leq 6$ takia muut arvot ovat mahdottomia sille.
Siksi E(y) = [-6;6].
$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Vastaus: E(f) = .
$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].
$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .
Muunnetaan lauseke $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.
Kosinin määritelmä tarkoittaa $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$
Koska tämä funktio on jatkuva koko määrittelyalueella, niin sen arvojen joukko on suljettu sen pienimmän ja suurimman arvon, jos sellainen on, funktion $y =\sqrt(2)\ arvojoukon väliin. cos((x +\frac(\pi)(4 )))$ on joukko $[-\sqrt(2);\sqrt(2)]$.
$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$
Merkitään $t = 5 – (3^(x)+1)^(2)$, missä -∞≤t≤4. Siten ongelma rajoittuu funktion $y = \log_(0,5)(t)$ arvojen joukon löytämiseen säteeltä (-∞;4). Koska funktio $y = \log_(0,5)(t)$ on määritetty vain arvolle t > 0, sen arvojoukko säteellä (-∞;4) osuu yhteen funktion arvojoukon kanssa. funktio välissä (0;4), joka edustaa on säteen (-∞;4) leikkauspiste logaritmisen funktion määritelmäalueen (0;+∞) kanssa. Välillä (0;4) tämä funktio on jatkuva ja laskeva. Kun t > 0, se pyrkii +∞, ja t = 4 saa arvon -2, joten E(y) = (-2, +∞).
Käytämme tekniikkaa, joka perustuu funktion graafiseen esitykseen.
Funktion muunnosten jälkeen saamme: y 2 + x 2 = 25 ja y ≥ 0, |x| ≤ 5.
On muistettava, että $x^(2)+y^(2)=r^(2)$ on ympyrän yhtälö, jonka säde on r.
Näillä rajoituksilla tämän yhtälön kuvaaja on ylempi puoliympyrä, jonka keskipiste on origossa ja jonka säde on 5. On selvää, että E(y) = .
Vastaus: E(y) = .
Viitteet
Tehtävien laajuus yhtenäisen valtiontutkinnon tehtävissä, Minyuk Irina Borisovna
Vinkkejä funktioarvojen joukon löytämiseen, Belyaeva I., Fedorova S.
Funktioarvojen joukon löytäminen
Kuinka ratkaista matematiikan ongelmia pääsykokeissa, I.I. Melnikov, I.N. Sergeev
Sivu 1
Oppitunti 3
"toimintoalue"
Tavoitteet: - Käytä arvoalueen käsitettä tietyn ongelman ratkaisuun;
ratkaisu tyypillisiä tehtäviä.
Useiden vuosien ajan on esiintynyt säännöllisesti ongelmia kokeissa, joissa tietystä funktioperheestä on valittava ne, joiden arvojoukot täyttävät ilmoitetut ehdot.
Mietitäänpä sellaisia tehtäviä.
Tiedon päivitys.
Mitä tarkoitamme funktioarvojen joukolla?
Mikä on funktion arvojoukko?
Mistä tiedoista löydämme funktioarvojen joukon? (Funktion tai sen kaavion analyyttisen merkinnän mukaan)
(cm KÄYTÄ tehtäviä, osa A)
Mitä funktioarvoja tiedämme? (Päätoiminnot on lueteltu taululle kirjoitettuna; kunkin funktion arvot on kirjoitettu ylös). Tuloksena taululle ja opiskelijoiden muistikirjoihin
|
Toiminto |
Monet arvot |
|
y = x 2 y = x 3 y=| x| y=
|
E( y) = E( y) = [- 1, 1] E( y) = (– ∞, + ∞) E( y) = (– ∞, + ∞) E( y) = (– ∞, + ∞) E( y) = (0, + ∞) |
Voimmeko tämän tiedon avulla löytää heti taululle kirjoitettujen funktioiden arvojoukot? (katso taulukko 2).
Mikä voi auttaa vastaamaan tähän kysymykseen? (Näiden funktioiden kaaviot).
Kuinka piirtää ensimmäinen funktio? (Laske paraabelia 4 yksikköä alaspäin).
|
Toiminto |
Monet arvot |
|
y = x 2 – 4 |
E( y) = [-4, + ∞) |
|
y = + 5 |
E( y) = |
|
y = – 5 cos x |
E( y) = [- 5, 5] |
|
y= tg( x + / 6) – 1 |
E( y) = (– ∞, + ∞) |
|
y= synti( x + / 3) – 2 |
E( y) = [- 3, - 1] |
|
y=| x – 1 | + 3 |
E( y) = |
|
y=| ctg x| |
E( y) = |
|
y =  = | cos(x + /4) | |
E( y) = |
|
y=(x- 5) 2 + 3 |
E( y) = . Etsi funktioarvojen joukko:   . 
Algoritmin esittely ongelmien ratkaisemiseksi trigonometristen funktioiden arvojoukon löytämiseksi. Katsotaanpa, kuinka voimme soveltaa kokemustamme yksittäisen kokeen vaihtoehtoihin sisältyviin erilaisiin tehtäviin. 1. Funktioiden arvojen löytäminen tietylle argumentin arvolle. Esimerkki. Etsi funktion arvo y = 2 cos(π/2+ π/4 ) – 1, Jos x = -π/2. Ratkaisu. y(-π/2) = 2 cos(- π/2 – π/4 )- 1= 2 cos(π/2 + π/4 )- 1 = - 2 syntiπ/4 – 1 = – 2  – 1 =
= – 2. Trigonometristen funktioiden alueen löytäminen
1≤ syntiX≤ 1 2 ≤ 2 syntiX≤ 2 9 ≤ 11+2syntiX≤ 13 3 ≤ Kirjoitetaan väliin funktion kokonaislukuarvot. Tämä luku on 3. Vastaus: 3.
klo= synti 2 X- 2 3 syntix + 3 2 - 3 2 + 8, klo= (syntiX- 3) 2 -1. E ( syntiX) = [-1;1]; E ( syntiX -3) = [-4;-2]; E ( syntiX -3) 2 = ; E ( klo) = . Vastaus:.
Voimmeko löytää arvojoukon tälle funktiolle? (Ei.) Mitä pitäisi tehdä? (Pennetty yhteen toimintoon.) Kuinka tehdä se? (Käytä kaavaa cos 2 x= 1-sin 2 x.) Niin, klo= 1-sin 2 x+2sin x –2, y= -sin 2 x+2sin x –1, klo= -(sin x –1) 2 . No, nyt voimme löytää joukon arvoja ja valita niistä pienimmän. 1 ≤ synti x ≤ 1, 2 ≤ synti x – 1 ≤ 0, 0 ≤ (sin x – 1) 2 ≤ 4, 4 ≤ -(sin x -1) 2 ≤ 0. Siis funktion pienin arvo klo vuokraus= -4. Vastaus: -4.
Ratkaisu. klo= 1-cos 2 x+ cos x + 1,5, klo= -cos 2 x+ 2∙0,5∙cos x - 0,25 + 2,75, klo= -(cos x- 0,5) 2 + 2,75. E(cos x) = [-1;1], E(cos x – 0,5) = [-1,5;0,5], E(cos x – 0,5) 2 = , E(-(cos x-0,5) 2) = [-2,25;0], E( klo) = . Funktion suurin arvo klo naib= 2,75; pienin arvo klo vuokraus= 0,5. Etsitään funktion suurimman ja pienimmän arvon tulo: klo naib ∙klo vuokraus = 0,5∙2,75 = 1,375. Vastaus: 1.375. Ratkaisu. Kirjoitetaan funktio uudelleen muotoon klo =, klo = Etsitään nyt funktion arvojoukko. E (sin x) = [-1, 1], E(6sin x) = [-6, 6], E(6sin x + 1) = [-5, 7], E((6sin x + 1) 2) = , E(– (6sin x + 1) 2) = [-49, 0], E(– (6sin x + 1) 2 + 64) = , E( y) = [ Etsitään funktion kokonaislukuarvojen summa: 4 + 5 + 6 + 7 + 8 = 30. Vastaus: 30.  Ratkaisu. 1) 2) Siksi 2 X kuuluvat toiselle neljännekselle. 3) Toisella vuosineljänneksellä sinifunktio pienenee ja on jatkuva. Tämä toiminto siis 4) Laske nämä arvot:
Vastaus :
 Ratkaisu. 1) Koska sini ottaa arvot välillä -1 arvoon 1, erotusarvojen joukko 2) Arkosiini on monotonisesti laskeva ja jatkuva funktio. Siksi lausekkeen arvojoukko on segmentti 3) Kun tämä segmentti kerrotaan Vastaus:  Ratkaisu. Koska arctangentti on kasvava funktio, niin 2) Kun kasvaa X alkaen 3) Kun kasvaa arvosta 4) Käyttämällä kaavaa, joka ilmaisee sinin puolikulman tangentin suhteen, löydämme sen
Siksi haluttu arvojoukko on segmenttien liitto Vastaus: klo= a sin x + b cos x tai klo= synti (Rx) + bcos (Rx).
Ratkaisu. Etsitään arvo Muunnetaan lauseke 15 sin 2x + 20 cos 2x = 25 ( 25 sin (2x + Funktioarvojen joukko y \u003d sin (2x + Sitten alkuperäisen funktion arvojen joukko -25 Vastaus:
[-25; 25].
Toiminto klo= ctg X pienenee segmentillä [π/4; π/2], joten funktio saa pienimmän arvon at x =π/2, eli klo(π/2) = сtg π/2 = 0; ja suurin arvo on x=π/4 eli klo(π/4) = сtg π/4 = 1. Vastaus: 1, 0.  . Ratkaisu. Erillään tasa-arvoisesti Tästä seuraa, että funktion f(x) kuvaaja on joko hyperboli (а≠ 0) tai suora ilman pistettä. Lisäksi, jos a; 2a) ja (2a; Jos a \u003d 0, niin f (x) \u003d -2 koko määritelmän alueella x ≠ 0. Siksi on selvää, että parametrin halutut arvot eivät ole nolla. Koska olemme kiinnostuneita vain segmentin [-1; 1], silloin tilanteiden luokittelu määräytyy sen perusteella, että hyperbolin asymptootti x = 2a (a≠0) sijaitsee suhteessa tähän segmenttiin. Tapaus 1. Kaikki intervallin [-1; 1] ovat pystyasymptootin oikealla puolella x = 2a, eli kun 2a Tapaus 2. Pystyasymptootti leikkaa intervallin [-1; 1], ja funktio pienenee (kuten tapauksessa 1), eli milloin Tapaus 3. Pystyasymptootti leikkaa intervallin [-1; 1] ja funktio kasvaa, eli -1 Tapaus 4. Kaikki intervallin [-1; 1] ovat pystyasymptootin vasemmalla puolella, eli 1 a > . ja toinen Vastaanotto 5. Murto-rationaalisen funktion määrittelevän kaavan yksinkertaistaminen Vastaanotto 6. Toisen asteen funktioiden arvojen joukon löytäminen (etsimällä paraabelin kärki ja määrittämällä sen haarojen käyttäytymisen luonne). Vastaanotto 7. Apukulman käyttöönotto joidenkin trigonometristen funktioiden arvojoukon löytämiseksi. Usein ongelmien ratkaisun puitteissa meidän on etsittävä funktion arvojoukkoa määritelmäalueelta tai segmentiltä. Tämä tulee tehdä esimerkiksi ratkaisemisen yhteydessä erilaisia tyyppejä epätasa-arvot, ilmaisuarviot jne. Osana tätä materiaalia kerromme sinulle, mikä funktion alue on, annamme tärkeimmät menetelmät, joilla se voidaan laskea, ja analysoimme monimutkaisia ongelmia. Selvyyden vuoksi yksittäiset sijainnit on havainnollistettu kaavioilla. Kun olet lukenut tämän artikkelin, sinulla on kattava käsitys toiminnon laajuudesta. Aloitetaan perusmääritelmistä. Määritelmä 1 Funktion y = f (x) arvojoukko jollain intervallilla x on kaikkien arvojen joukko, jotka tämä funktio ottaa, kun iteroidaan kaikkien x ∈ X -arvojen yli. Määritelmä 2 Funktion y = f (x) alue on joukko sen arvoja, jotka se voi ottaa, kun iteroidaan arvojen x yli alueelta x ∈ (f) . Jonkin funktion alue on yleensä merkitty E (f) . Huomaa, että funktion arvojoukon käsite ei aina ole identtinen sen arvojen alueen kanssa. Nämä käsitteet ovat samanarvoisia vain, jos x-arvojen alue arvojoukkoa löydettäessä osuu yhteen funktion toimialueen kanssa. On myös tärkeää erottaa muuttujan x vaihteluväli oikealla puolella olevalle lausekkeelle y = f (x) . Lausekkeen f (x) hyväksyttävien arvojen x alue on tämän funktion määritysalue. Alla on kuva, jossa on esimerkkejä. Siniset viivat ovat funktioiden kuvaajia, punaiset asymptootteja, punaiset pisteet ja viivat y-akselilla ovat funktion alueita. On selvää, että funktion alue voidaan saada projisoimalla funktion kuvaaja akselille O y . Samaan aikaan se voi olla joko yksittäinen luku tai joukko numeroita, segmentti, intervalli, avoin säde, numeeristen intervallien liitto jne. Harkitse tärkeimpiä tapoja löytää funktion alue. Aloitetaan määrittämällä jatkuvan funktion y = f (x) arvot tietylle segmentille, joka on merkitty [ a ; b]. Tiedämme, että funktio, joka on jatkuva tietyllä aikavälillä, saavuttaa sillä minimi- ja maksiminsa, eli maksiminsa m a x x ∈ a ; b f (x) ja pienin arvo m i n x ∈ a ; b f (x) . Joten saamme janan m i n x ∈ a ; bf(x) ; m a x x ∈ a ; b f (x) , joka sisältää alkuperäisen funktion arvojoukot. Sitten meidän tarvitsee vain löytää määritetyt minimi- ja maksimipisteet tästä segmentistä. Otetaan ongelma, jossa on tarpeen määrittää arsinin arvoalue. Esimerkki 1 Kunto: etsi alue y = a r c sin x . Ratkaisu Yleisessä tapauksessa arsinin määritelmäalue sijaitsee välissä [-1 ; 1]. Meidän on määritettävä sille määritetyn funktion suurin ja pienin arvo. y "= a r c sin x" = 1 1 - x 2 Tiedämme, että funktion derivaatta on positiivinen kaikille x-arvoille, jotka sijaitsevat välissä [-1; 1 ] , eli koko määrittelyalueen arksinifunktio kasvaa. Tämä tarkoittaa, että se ottaa pienimmän arvon, kun x on yhtä suuri kuin -1, ja suurimman - kun x on yhtä suuri kuin 1. m i n x ∈ - 1; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2 Siten arsinifunktion alue on yhtä suuri kuin E (a r c sin x) = - π 2 ; π2. Vastaus: E (a r c sin x) \u003d - π 2; π 2 Esimerkki 2 Kunto: laske alue y = x 4 - 5 x 3 + 6 x 2 annetulle segmentille [ 1 ; 4]. Ratkaisu Meidän tarvitsee vain laskea funktion suurin ja pienin arvo annetulla aikavälillä. Ääripisteiden määrittämiseksi on suoritettava seuraavat laskelmat: y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 ja l ja 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1 ;4 ;x3 = 15 + 338 ≈ 2,59 ∈ 1;4 Etsitään nyt annetun funktion arvot janan päistä ja pisteistä x 2 = 15 - 33 8 ; x 3 \u003d 15 + 33 8: y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 v 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 ≈ + 165 33 512 2. 08 v 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 v (4) = 4 4 - 5 4 3 + 6 4 2 = 32 Tämä tarkoittaa, että funktioarvot määritetään segmentillä 117 - 165 33 512 ; 32 . Vastaus: 117 - 165 33 512 ; 32 . Siirrytään etsimään jatkuvan funktion y = f (x) arvojen joukko väliltä (a ; b) ja a ; + ∞ , - ∞ ; b , -∞ ; +∞ . Aloitetaan määrittämällä suurimmat ja pienimmät pisteet sekä lisäys- ja laskuvälit tietyllä aikavälillä. Sen jälkeen meidän on laskettava yksipuoliset rajat intervallin päissä ja/tai rajat äärettömyydessä. Toisin sanoen meidän on määritettävä funktion käyttäytyminen tietyissä olosuhteissa. Tätä varten meillä on kaikki tarvittavat tiedot. Esimerkki 3 Kunto: laske funktion alue y = 1 x 2 - 4 välillä (- 2 ; 2) . Ratkaisu Määritä funktion suurin ja pienin arvo tietyllä aikavälillä y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2) Saimme maksimiarvon, joka on yhtä suuri kuin 0 , koska tässä vaiheessa funktion etumerkki muuttuu ja kuvaaja alkaa pienentyä. Katso kuva:
Eli y (0) = 1 0 2 - 4 = - 1 4 on funktion maksimiarvo. Määritetään nyt funktion käyttäytyminen x:lle, joka pyrkii olemaan -2 oikealla puolella ja +2 vasemmalla puolella. Toisin sanoen löydämme yksipuolisia rajoja: lim x → - 2 + 0 1 x 2 - 4 = raja x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = raja x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞ Saimme, että funktion arvot kasvavat miinus äärettömästä arvoon -1 4, kun argumentti muuttuu arvosta -2 arvoon 0. Ja kun argumentti muuttuu 0:sta 2:ksi, funktion arvot pienenevät kohti miinus ääretöntä. Siksi tietyn funktion arvojen joukko tarvitsemamme välissä on (- ∞ ; - 1 4 ] . Vastaus: (- ∞ ; - 1 4 ] . Esimerkki 4 Kunto: osoita arvojen joukko y = t g x annetulla välillä - π 2 ; π2. Ratkaisu Tiedämme, että yleensä tangentin derivaatta in - π 2; π 2 on positiivinen, eli funktio kasvaa. Määritetään nyt kuinka funktio käyttäytyy annetuissa rajoissa: lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞ Olemme saaneet funktion arvojen kasvun miinus äärettömyydestä plus äärettömään, kun argumentti muuttuu arvosta - π 2 arvoon π 2, ja voimme sanoa, että tämän funktion ratkaisujen joukko on kaikkien reaalien joukko. numeroita. Vastaus: - ∞ ; + ∞ . Esimerkki 5 Kunto: määritä mikä on luonnollisen logaritmifunktion y = ln x alue. Ratkaisu Tiedämme, että tämä funktio on määritelty argumentin D (y) = 0 positiivisille arvoille; +∞ . Annetun välin derivaatta on positiivinen: y " = ln x " = 1 x . Tämä tarkoittaa, että sen toiminto kasvaa. Seuraavaksi meidän on määritettävä yksipuolinen raja tapaukselle, jossa argumentti menee 0:aan (oikealla puolella) ja kun x menee äärettömään: lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞ Olemme havainneet, että funktion arvot kasvavat miinus äärettömyydestä plus äärettömään, kun x-arvot muuttuvat nollasta plus äärettömään. Tämä tarkoittaa, että kaikkien reaalilukujen joukko on luonnollisen logaritmifunktion alue. Vastaus: kaikkien reaalilukujen joukko on luonnollisen logaritmifunktion alue. Esimerkki 6 Kunto: määritä mikä on funktion y = 9 x 2 + 1 alue. Ratkaisu Tämä funktio on määritelty, jos x on reaaliluku. Lasketaan funktion suurimmat ja pienimmät arvot sekä sen kasvun ja laskun välit: y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0 Tämän seurauksena olemme päättäneet, että tämä funktio pienenee, jos x ≥ 0; kasvaa, jos x ≤ 0 ; sillä on maksimipiste y (0) = 9 0 2 + 1 = 9, kun muuttuja on 0 . Katsotaan kuinka funktio käyttäytyy äärettömässä: lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0 Tietueesta voidaan nähdä, että funktion arvot lähestyvät tässä tapauksessa asymptoottisesti nollaa. Yhteenvetona: kun argumentti muuttuu miinus äärettömästä nollaan, funktion arvot kasvavat 0:sta 9:ään. Kun argumenttiarvot muuttuvat 0:sta plus äärettömään, vastaavat funktioarvot pienenevät arvosta 9 arvoon 0. Olemme kuvanneet tämän kuvassa:
Se osoittaa, että funktion alue on väli E (y) = (0 ; 9 ] Vastaus: E (y) = (0 ; 9 ] Jos meidän on määritettävä funktion y = f (x) arvot intervalleilla [ a ; b) , (a ; b ] , [a ; + ∞) , (- ∞ ; b ] , silloin meidän on suoritettava täsmälleen samat tutkimukset. Emme analysoi näitä tapauksia vielä, vaan kohtaamme ne myöhemmin ongelmissa . Mutta entä jos tietyn funktion alue on useiden intervallien liitto? Sitten meidän on laskettava arvojoukot jokaiselle näistä intervalleista ja yhdistettävä ne. Esimerkki 7 Kunto: määritä mikä on y = x x - 2 : n alue . Ratkaisu Koska funktion nimittäjää ei saa muuttaa 0:ksi, niin D (y) = - ∞ ; 2 ∪ 2; +∞ . Aloitetaan määrittämällä funktioarvot ensimmäiselle segmentille - ∞ ; 2, joka on avoin palkki. Tiedämme, että sen funktio pienenee, eli tämän funktion derivaatta on negatiivinen. lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0 Silloin niissä tapauksissa, joissa argumentti muuttuu kohti miinus ääretöntä, funktion arvot lähestyvät asymptoottisesti arvoa 1 . Jos x:n arvot muuttuvat miinus äärettömästä 2:ksi, arvot pienenevät 1:stä miinus äärettömyyteen, ts. tämän segmentin funktio ottaa arvot väliltä - ∞ ; 1 . Jätämme yhtenäisyyden pois päättelystämme, koska funktion arvot eivät saavuta sitä, vaan lähestyvät sitä vain asymptoottisesti. Avoimelle palkkille 2 ; + ∞ suoritamme täsmälleen samat toiminnot. Myös sen toiminto vähenee: lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0 Tämän segmentin funktion arvot määrää joukko 1 ; +∞ . Tämä tarkoittaa, että tarvitsemamme ehdolla määritetyn funktion arvoalue on joukkojen liitto - ∞; 1 ja 1; +∞ . Vastaus: E(y) = -∞; 1 ∪ 1; +∞ . Tämä näkyy kaaviossa:
Erikoistapaus ovat jaksolliset funktiot. Niiden arvoalue on sama kuin arvojoukon välissä, joka vastaa tämän toiminnon jaksoa. Esimerkki 8 Kunto: määritä sinin y = sin x alue. Ratkaisu Sini viittaa jaksolliseen funktioon ja sen jakso on 2 pi. Otetaan segmentti 0 ; 2 π ja katso, mikä sen arvojoukko tulee olemaan. y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z 0 sisällä; 2 π funktiolla on ääripisteet π 2 ja x = 3 π 2 . Lasketaan, mitkä funktion arvot ovat yhtä suuria niissä, samoin kuin segmentin rajoilla, minkä jälkeen valitsemme suurimman ja pienimmän arvon. y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1, max x ∈ 0; 2 π sinx \u003d sin π 2 \u003d 1 Vastaus: E (sinx) = -1; 1 . Jos sinun on tiedettävä funktioalueet, kuten eksponentiaalinen, eksponentiaalinen, logaritminen, trigonometrinen, käänteinen trigonometrinen, suosittelemme lukemaan uudelleen artikkelin perusfunktioista. Tässä esittämämme teoria antaa meille mahdollisuuden testata siellä määritettyjä arvoja. Ne kannattaa opetella, koska niitä tarvitaan usein ongelmien ratkaisemisessa. Jos tiedät pääfunktioiden alueet, voit helposti löytää perusfunktioista geometrisen muunnoksen avulla saadut funktioalueet. Esimerkki 9 Kunto: määritä alue y = 3 a r c cos x 3 + 5 π 7 - 4 . Ratkaisu Tiedämme, että segmentti 0:sta pi:hen on käänteiskosinin alue. Toisin sanoen E (a r c cos x) = 0 ; π tai 0 ≤ a r c cos x ≤ π . Voimme saada funktion a r c cos x 3 + 5 π 7 kaarikosinista siirtämällä ja venyttämällä sitä O x -akselia pitkin, mutta tällaiset muunnokset eivät anna meille mitään. Siten 0 ≤ a r c cos x 3 + 5 π 7 ≤ π . Funktio 3 a r c cos x 3 + 5 π 7 saadaan käänteiskosinista a r c cos x 3 + 5 π 7 venyttämällä pitkin y-akselia, ts. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Lopullinen muunnos on siirtymä O y -akselia pitkin 4 arvolla. Tuloksena saamme kaksinkertaisen epätasa-arvon: 0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 kaaria x 3 + 5 π 7 - 4 ≤ 3 π - 4 Saimme, että tarvitsemamme alue on yhtä suuri kuin E (y) = - 4 ; 3 pi - 4 . Vastaus: E(y) = -4; 3 pi - 4 . Kirjoitetaan vielä yksi esimerkki ilman selityksiä, koska se on täysin samanlainen kuin edellinen. Esimerkki 10 Kunto: laske mikä on funktion y = 2 2 x - 1 + 3 alue. Ratkaisu Kirjoitetaan ehdolla annettu funktio uudelleen muotoon y = 2 · (2 × - 1) - 1 2 + 3 . Potenttifunktiolle y = x - 1 2 alue määritellään välillä 0 ; + ∞ ts. x - 1 2 > 0 . Tässä tapauksessa: 2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3 Joten E(y) = 3; +∞ . Vastaus: E(y) = 3; +∞ . Katsotaan nyt kuinka löytää funktion alue, joka ei ole jatkuva. Tätä varten meidän on jaettava koko alue intervalleiksi ja löydettävä arvojoukot jokaiselle niistä ja yhdistettävä sitten se, mitä meillä on. Ymmärtääksesi tämän paremmin, suosittelemme tutustumaan funktioiden keskeytyskohtien päätyyppeihin. Esimerkki 11 Kunto: annettu funktio y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3. Laske sen alue. Ratkaisu Tämä funktio on määritetty kaikille x-arvoille. Analysoidaan sitä jatkuvuuden suhteen argumentin arvoilla, jotka ovat yhtä suuria kuin - 3 ja 3: lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x) Meillä on ensimmäisen tyyppinen korjaamaton epäjatkuvuus argumentin -3 arvon kanssa. Kun lähestyt sitä, funktion arvoilla on taipumus olla -2 sin 3 2 - 4, ja kun x oikealla puolella on -3, arvot yleensä -1. lim x → 3 - 0 f(x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f(x) = lim x → 3 + 0 1 x - 3 = + ∞ Meillä on toista tyyppiä oleva poistamaton katkonaisuus kohdassa 3. Kun funktio pyrkii siihen, sen arvot lähestyvät -1:tä, kun taas samaan pisteeseen oikealla - miinus äärettömään. Tämä tarkoittaa, että tämän funktion koko määrittelyalue on jaettu 3 väliin (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) ). Ensimmäisellä niistä saimme funktion y \u003d 2 sin x 2 - 4. Koska -1 ≤ sin x ≤ 1 , saamme: 1 ≤ sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2 Tämä tarkoittaa, että tällä välillä (- ∞ ; - 3 ] funktion arvojoukko on [ - 6 ; 2 ] . Puolivälillä (- 3 ; 3 ] saadaan vakiofunktio y = - 1 . Näin ollen koko sen arvojen joukko tässä tapauksessa pienenee yhdeksi numeroksi - 1 . Toisella aikavälillä 3; + ∞ meillä on funktio y = 1 x - 3 . Se pienenee, koska y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что: lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0 Tästä syystä alkuperäisen funktion arvojoukko x > 3:lle on joukko 0 ; +∞ . Yhdistetään nyt tulokset: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0; +∞ . Vastaus: E(y) = -6; - 2 ∪ - 1 ∪ 0; +∞ . Ratkaisu näkyy kaaviossa:
Esimerkki 12 Ehto: on olemassa funktio y = x 2 - 3 e x . Määritä sen arvojen joukko. Ratkaisu Se määritellään kaikille argumenttiarvoille, jotka ovat reaalilukuja. Määritetään, millä aikaväleillä tämä funktio kasvaa ja missä se vähenee: y "= x 2 - 3 e x" = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x Tiedämme, että derivaatasta tulee 0, jos x = -1 ja x = 3. Sijoitamme nämä kaksi pistettä akselille ja selvitämme, mitkä merkit derivaatalla on tuloksena olevilla intervalleilla.
Funktio pienenee (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) ja kasvaa [ - 1 ; 3]. Pienin piste on -1, maksimi -3. Etsitään nyt vastaavat funktioarvot: y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3 Katsotaanpa funktion käyttäytymistä äärettömässä: lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 "e x" = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x "(e x)" = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0 Toisen rajan laskemiseen käytettiin L'Hopitalin sääntöä. Piirretään ratkaisumme kaavioon.
Se osoittaa, että funktion arvot pienenevät plus äärettömästä arvoon -2 e, kun argumentti muuttuu miinus äärettömästä arvoon -1. Jos se muuttuu 3:sta plus äärettömään, arvot laskevat arvosta 6 e - 3 arvoon 0, mutta nollaa ei saavuteta. Siten E(y) = [-2e; +∞) . Vastaus: E(y) = [-2e; +∞) Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter |
– 1.
, eli E (y) = .
,
, 8].
tuo on X kuuluu ensimmäiseen neljännekseen.
ennen 
.
. Kun kerrotaan 
tämä segmentti siirtyy segmenttiin 
.
.
saamme 
.
.
.
ennen 
argumentti 2 X kasvaa alkaen 
ennen 
. Koska sini tällaisella intervallilla kasvaa, funktio 
1 asti.
argumentti 2 X kasvaa alkaen 
. Koska sini pienenee sellaisella aikavälillä, funktio 
1 asti.
.
Ja 
, eli segmentti 
= 
= 25.
) = 25 () =
), missä cos 
synti (2x + 
) ja jos a > 0, kasvaa monotonisesti näillä säteillä.
.
