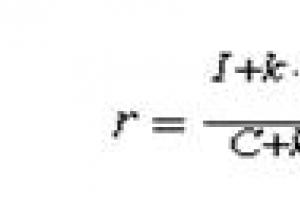موضوع الدرس هو "مجموعة قيم الوظائف في مشاكل الاستخدام. إيجاد مجموعة قيم الدالة مجموعة قيم الدالة y 4 x

سننتقل اليوم في الدرس إلى أحد المفاهيم الأساسية للرياضيات - مفهوم الوظيفة ؛ دعنا نلقي نظرة فاحصة على إحدى خصائص الدالة - مجموعة قيمها.

خلال الفصول

مدرس. عند حل المشكلات ، نلاحظ أنه في بعض الأحيان يكون البحث الدقيق عن مجموعة قيم دالة يضعنا في مواقف صعبة. لماذا؟ يبدو أن دراسة الوظيفة من الصف السابع ، نعرف الكثير عنها. لذلك ، لدينا كل الأسباب لاتخاذ خطوة استباقية. دعونا "نلعب" مع الكثير من قيم الوظائف اليوم لحل العديد من الأسئلة حول هذا الموضوع في الاختبار القادم.

مجموعات من قيم الوظائف الأولية

مدرس. بادئ ذي بدء ، من الضروري تكرار الرسوم البيانية والمعادلات ومجموعات قيم الوظائف الأولية الأساسية على نطاق التعريف بأكمله.

يتم عرض الرسوم البيانية للوظائف على الشاشة: خطي ، تربيعي ، كسري منطقي ، مثلثي ، أسي ولوغاريتمي ، لكل منها مجموعة من القيم يتم تحديدها شفهيًا. انتبه إلى حقيقة أن الدالة الخطية E (f) = رأو رقم واحد للكسر الخطي

هذه أبجديةنا. من خلال إضافة معرفتنا بتحولات الرسم البياني: الترجمة المتوازية ، والتمدد ، والضغط ، والانعكاس ، يمكننا حل مشاكل الجزء الأول الاستخدام وحتى أكثر صعوبة بقليل. دعونا التحقق من ذلك.

عمل مستقل

في كلمات المهمة وأنظمة الإحداثيات المطبوعة لكل طالب.

1. ابحث عن مجموعة قيم الوظائف في مجال التعريف بالكامل:

أ) ذ= 3 خطيئة X ;
ب) ذ = 7 – 2 X ;
الخامس) ذ= -arccos ( x + 5):
ز) ذ= | arctg x |;
ه)

2. ابحث عن مجموعة قيم الوظيفة ذ = x 2 بينهما ي، لو:

أ) ي = ;
ب) ي = [–1; 5).

3. حدد دالة تحليليًا (بواسطة معادلة) إذا كانت مجموعة قيمها:

1) ه(F(x)) = (–∞؛ 2] و F(x) - وظيفة

مربع
ب) لوغاريتمي ،
ج) برهاني.

2) ه(F(x)) = ر \{7}.

عند مناقشة مهمة 2في العمل المستقل ، لفت انتباه الطلاب إلى حقيقة أنه في حالة الرتابة واستمرارية الوظيفة y=F(x)في فترة زمنية معينة[أ;ب],مجموعة معانيها-فجوة,نهاياتها هي القيم و(أ)و(ب).

خيارات الإجابة للمهمة 3.

1.
أ) ذ = –x 2 + 2 , ذ = –(x + 18) 2 + 2,
ذ= أ(x – xج) 2 + 2 في أ < 0.

ب) ذ= - | سجل 8 x | + 2,

الخامس) ذ = –| 3 x – 7 | + 2, ذ = –5 | x | + 3.

2.
أ) ب)

الخامس) ذ = 12 – 5x، أين x ≠ 1 .

إيجاد مجموعة قيم دالة باستخدام المشتق

مدرس. في الصف العاشر ، تعرفنا على الخوارزمية لإيجاد القيمة القصوى لدالة متصلة على مقطع ما وإيجاد مجموعة قيمها دون الاعتماد على الرسم البياني للدالة. تذكر كيف فعلنا ذلك؟ ( بمساعدة المشتق.) دعنا نتذكر هذه الخوارزمية .

1. تأكد من الوظيفة ذ = F(x) محدد ومستمر على المقطع ي = [أ; ب]. 2. ابحث عن قيم الوظيفة في نهايات المقطع: و (أ) و (ب). تعليق. إذا علمنا أن الوظيفة مستمرة ورتيبة ي، ثم يمكنك الإجابة على الفور: ه(F) = [F(أ); F(ب)] أو ه(F) = [F(ب); F(أ)]. 3. أوجد المشتق ثم النقاط الحرجة س كي. 4. البحث عن قيم دالة في النقاط الحرجة F(س ك). 5. قارن قيم الدالة F(أ), F(ب) و F(س ك) ، اختر أكبر وأصغر قيم للدالة وأعطي إجابة: ه(F)= [Fيؤجر؛ Fنيب].

تم العثور على مشاكل تطبيق هذه الخوارزمية في خيارات الاستخدام. على سبيل المثال ، في عام 2008 تم اقتراح مثل هذه المهمة. عليك أن تحلها منازل .

المهمة C1.أوجد أكبر قيمة لدالة

F(x) = (0,5x + 1) 4 – 50(0,5x + 1) 2

في | x + 1| ≤ 3.

طباعة شروط الواجب المنزلي لكل طالب .

إيجاد مجموعة قيم دالة معقدة

مدرس. سيكون الجزء الرئيسي من درسنا هو المهام غير القياسية التي تحتوي على وظائف معقدة ، ومشتقاتها عبارة عن تعبيرات معقدة للغاية. والرسوم البيانية لهذه الدوال غير معروفة لنا. لذلك ، بالنسبة للحل ، سنستخدم تعريف دالة معقدة ، أي الاعتماد بين المتغيرات في ترتيب تداخلها في هذه الوظيفة ، وتقييم نطاقها (فترة التغيير في قيمها). تم العثور على مشاكل من هذا النوع في الجزء الثاني من الاختبار. دعنا ننتقل إلى الأمثلة.

التمرين 1.للوظائف ذ = F(x) و ذ = ز(x) اكتب دالة معقدة ذ = F(ز(x)) وابحث عن مجموعة قيمها:

أ) F(x) = –x 2 + 2x + 3, ز(x) = الخطيئة x;
ب) F(x) = –x 2 + 2x + 3, ز(x) = تسجيل 7 x;
الخامس) ز(x) = x 2 + 1;
ز)

حل.أ) الوظيفة المعقدة لها الشكل: ذ= -sin 2 x+ 2sin x + 3.

تقديم وسيطة وسيطة ر، يمكننا كتابة هذه الوظيفة على النحو التالي:

ذ= –ر 2 + 2ر+ 3 أين ر= الخطيئة x.

في الوظيفة الداخلية ر= الخطيئة xتأخذ الوسيطة أي قيمة ، ومجموعة قيمها هي المقطع [–1 ؛ 1].

لذلك بالنسبة للوظيفة الخارجية ذ = –ر 2 +2ر+ 3 لقد تعلمنا الفاصل الزمني لتغيير قيم حجته ر: ر[-1 ؛ 1]. لنلقِ نظرة على الرسم البياني للدالة ذ = –ر 2 +2ر + 3.

لاحظ أن الدالة التربيعية لـ ر[-1 ؛ 1] يأخذ القيم الأصغر والأكبر في نهايته: ذالتوظيف = ذ(-1) = 0 و ذنيب = ذ(1) = 4. وبما أن هذه الوظيفة متصلة على المجال [–1؛ 1] ، ثم يأخذ أيضًا جميع القيم بينهما.

إجابة: ذ .

ب) يقودنا تكوين هذه الوظائف إلى وظيفة معقدة يمكن ، بعد تقديم وسيطة ، تمثيلها على النحو التالي:

ذ= –ر 2 + 2ر+ 3 أين ر= سجل 7 x,

وظيفة ر= سجل 7 x

x (0; +∞ ), ر (–∞ ; +∞ ).

وظيفة ذ = –ر 2 + 2ر+ 3 (انظر الرسم البياني) وسيطة رتأخذ أي قيمة ، والدالة التربيعية نفسها تأخذ جميع القيم التي لا تزيد عن 4.

إجابة: ذ (–∞ ; 4].

ج) الوظيفة المعقدة لها الشكل التالي:

عند تقديم وسيطة ، نحصل على:

أين ر = x 2 + 1.

منذ ذلك الحين للوظيفة الداخلية x ر ، أ ر .

إجابة: ذ (0; 3].

د) تكوين هاتين الوظيفتين يعطينا وظيفة معقدة

والتي يمكن كتابتها كـ

لاحظ أن

لذلك ، في

أين ك ض , ر [–1; 0) (0; 1].

رسم رسم بياني للدالة نرى ذلك لهذه القيم ر

ذ(–∞ ؛ –4] ج ؛

ب) على كامل مجال التعريف.

حل.أولاً ، نفحص هذه الوظيفة من أجل الرتابة. وظيفة ر= أركتج x- مستمر ومتناقص ر ومجموعة قيمها (0 ؛ π). وظيفة ذ= سجل 5 ريتم تعريفه على الفاصل الزمني (0 ؛ π) ، وهو مستمر ويزيد عليه. هذا يعني أن هذه الدالة المعقدة تتناقص في المجموعة ر . وهو ، كتكوين لوظيفتين مستمرتين ، سيكون مستمرًا ر .

دعونا نحل المشكلة "أ".

نظرًا لأن الوظيفة متصلة على خط الأعداد بالكامل ، فهي متصلة في أي جزء منها ، على وجه الخصوص ، في مقطع معين. ثم في هذا المقطع يحتوي على أصغر وأكبر القيم ويأخذ كل القيم بينهما:

F(4) = log 5 arcctg 4.

أي من القيم الناتجة أكبر؟ لماذا؟ وماذا ستكون مجموعة القيم؟

إجابة:

لنحل المشكلة "ب".

إجابة: في(– ؛ سجل 5 π) في جميع أنحاء مجال التعريف.

مهمة مع المعلمة

لنحاول الآن إنشاء معادلة بسيطة وحلها باستخدام معلمة من النموذج F(x) = أ، أين F(x) - نفس الوظيفة كما في المهمة 4.

المهمة 5.حدد عدد جذور معادلة log 5 (arcctg x) = ألكل قيمة معلمة أ.

حل.كما أوضحنا بالفعل في المهمة 4 ، الوظيفة في= سجل 5 (arctg x) يتناقص ومستمر على ر ويأخذ قيمًا أقل من log 5 π. هذه المعلومات كافية لإعطاء إجابة.

إجابة:لو أ < log 5 π, то уравнение имеет единственный корень;

لو أ≥ log 5 π ، فلا توجد جذور.

مدرس. لقد درسنا اليوم المشكلات المتعلقة بإيجاد مجموعة قيم الوظيفة. في هذا المسار ، اكتشفنا طريقة جديدة لحل المعادلات وعدم المساواة - طريقة التقدير ، لذا أصبح إيجاد مجموعة قيم دالة ما وسيلة لحل المشكلات ذات المستوى الأعلى. في الوقت نفسه ، رأينا كيف يتم إنشاء مثل هذه المشكلات وكيف تسهل خصائص الرتابة للوظيفة حلها.

وأتمنى أن يكون المنطق الذي ربط المهام المدروسة اليوم قد فاجأك ، أو على الأقل فاجأك. لا يمكن أن يكون الأمر خلاف ذلك: تسلق قمة جديدة لا يترك أي شخص غير مبال! نلاحظ ونقدر اللوحات والمنحوتات الجميلة وما إلى ذلك. لكن للرياضيات أيضًا جمالها الخاص وجاذبيتها وساحرها - جمال المنطق. علماء الرياضيات يقولون ذلك حل جميل- هذا عادة الحل الصحيحوهي ليست مجرد عبارة. الآن عليك أن تجد مثل هذه الحلول ، وقد أوضحنا إحدى الطرق لها اليوم. كل التوفيق لك! وتذكر: الطريق سوف يتقن السير على الأقدام!

الوظيفة هي النموذج. دعنا نعرّف X على أنها مجموعة من قيم المتغير المستقل // يعني أي مستقل.

الوظيفة هي قاعدة يمكن بواسطتها ، لكل قيمة من المتغير المستقل من المجموعة X ، العثور على القيمة الوحيدة للمتغير التابع. // أي. لكل x هناك واحد y.

ويترتب على التعريف أن هناك مفهومين - متغير مستقل (نشير إليه بواسطة x ويمكن أن يأخذ أي قيمة) ومتغير تابع (نشير إليه بواسطة y أو f (x) ويتم حسابه من الوظيفة عندما نستبدل x).

على سبيل المثال y = 5 + x

1. المستقل هو x ، لذلك نأخذ أي قيمة ، لنفترض أن x = 3

2. والآن نحسب y ، لذا y \ u003d 5 + x \ u003d 5 + 3 \ u003d 8. (y تعتمد على x ، لأن ما س نعوض به ، نحصل على y)

نقول أن المتغير y يعتمد وظيفيًا على المتغير x وهذا يُشار إليه على النحو التالي: y = f (x).

على سبيل المثال.

1. ص = 1 / س. (يسمى الغلو)

2. ص = س ^ 2. (تسمى القطع المكافئ)

3. ص = 3 س + 7. (يسمى الخط المستقيم)

4. ص \ u003d √ س. (يسمى فرع القطع المكافئ)

المتغير المستقل (الذي نشير إليه بواسطة x) يسمى وسيطة الوظيفة.

نطاق الوظيفة

تسمى مجموعة جميع القيم التي تأخذها وسيطة الوظيفة مجال الوظيفة ويتم الإشارة إليها بواسطة D (f) أو D (y).

ضع في اعتبارك D (y) من أجل 1. ، 2. ، 3. ، 4.

1. D (y) = (∞؛ 0) و (0؛ +) // المجموعة الكاملة من الأعداد الحقيقية باستثناء الصفر.

2. D (y) \ u003d (∞ ؛ + ∞) / / جميع الأرقام الحقيقية العديدة

3. D (y) \ u003d (∞ ؛ + ∞) / / كل الأرقام الحقيقية العديدة

4. D (ص) \ u003d. أوجد أكبر وأصغر قيمة للدالة في هذا المقطع.

المشتق موجب للجميع xمن الفاصل (-1; 1) ، وهذا يعني أن وظيفة القوسين تزداد على نطاق التعريف بأكمله. لذلك ، يأخذ أصغر قيمة عند س = -1، والأكبر في س = 1.

حصلنا على نطاق دالة القوسين .

أوجد مجموعة قيم الدالة في الجزء .

حل.

أوجد أكبر وأصغر قيمة للدالة في المقطع المحدد.

دعونا نحدد النقاط القصوى التي تنتمي إلى المقطع :

يسمى اعتماد متغير واحد على آخر التبعية الوظيفية.تبعية متغيرة ذمن متغير xمُسَمًّى وظيفة، إذا كانت كل قيمة xيطابق قيمة واحدة ذ.

تعيين:

عامل xيسمى المتغير المستقل أو دعوى، والمتغير ذ- متكل. ويقولون ان ذهي وظيفة x. معنى ذالمقابلة للقيمة المعطاة x، مُسَمًّى قيمة الوظيفة.

كل القيم التي يأخذها x، استمارة نطاق الوظيفة؛ كل القيم التي يأخذها ذ، استمارة مجموعة من القيم الوظيفية.

التعيينات:

د (و)- قيم الحجة. ه (و)- قيم الدالة. إذا تم إعطاء الوظيفة بواسطة صيغة ، فيُعتبر أن مجال التعريف يتكون من جميع قيم المتغير التي تكون هذه الصيغة منطقية لها.

رسم بياني وظيفييتم استدعاء مجموعة جميع النقاط على مستوى الإحداثيات ، حيث تكون الأحرف الخاصة بها مساوية لقيم الوسيطة ، وتكون الإحداثيات مساوية للقيم المقابلة للوظيفة. إذا كانت بعض القيمة س = x0تطابق قيم متعددة (ليست واحدة فقط) ذ، إذن هذه المراسلات ليست وظيفة. لكي تكون مجموعة نقاط المستوى الإحداثي رسمًا بيانيًا لبعض الوظائف ، من الضروري والكافي أن يتقاطع أي خط مستقيم موازٍ لمحور Oy مع الرسم البياني عند نقطة واحدة على الأكثر.

طرق لتعيين وظيفة

1) يمكن ضبط الوظيفة تحليليافي شكل صيغة. على سبيل المثال،

2) يمكن تحديد الوظيفة بجدول من عدة أزواج (س ؛ ص).

3) يمكن تعيين الوظيفة بيانيا. أزواج القيمة (س ؛ ص)معروضة على مستوى الإحداثيات.

رتابة الوظيفة

وظيفة و (خ)مُسَمًّى في ازديادفي فترة عددية معينة ، إذا كانت القيمة الأكبر للوسيطة تتوافق مع قيمة أكبر للدالة. تخيل أن نقطة معينة تتحرك على طول الرسم البياني من اليسار إلى اليمين. ثم سترتفع النقطة نوعًا ما لأعلى على الرسم البياني.

وظيفة و (خ)مُسَمًّى يتضاءلفي فترة عددية معينة ، إذا كانت القيمة الأكبر للوسيطة تتوافق مع قيمة أصغر للدالة. تخيل أن نقطة معينة تتحرك على طول الرسم البياني من اليسار إلى اليمين. ثم ستدحرج النقطة ، كما كانت ، على الرسم البياني.

يتم استدعاء الوظيفة التي تتزايد أو تتناقص فقط في فترة عددية معينة رتيبفي هذه الفترة.

أصفار الدالة وفترات الثبات

قيم X، الذي ص = 0، يسمى وظيفة الأصفار. هذه هي الخطوط العريضة لنقاط تقاطع الرسم البياني للدالة مع المحور x.

نطاقات القيم هذه x، حيث قيم الدالة ذيتم استدعاء إما إيجابية فقط أو سلبية فقط فترات ثبات الإشارة للوظيفة.

الوظائف الفردية والزوجية

دالة زوجية
1) مجال التعريف متماثل فيما يتعلق بالنقطة (0 ؛ 0) ، أي إذا كانت النقطة أينتمي إلى مجال التعريف ، ثم النقطة -أينتمي أيضا إلى مجال التعريف.
2) لأي قيمة x و (-x) = و (س)
3) الرسم البياني للدالة الزوجية متماثل حول محور Oy.

وظيفة غريبةله الخصائص التالية:
1) مجال التعريف متماثل بالنسبة للنقطة (0 ؛ 0).
2) لأي قيمة x، التي تنتمي إلى مجال التعريف ، المساواة و (-x) = - و (س)
3) الرسم البياني للدالة الفردية متماثل فيما يتعلق بالأصل (0 ؛ 0).

ليست كل وظيفة زوجية أو فردية. المهام نظرة عامةليست زوجية ولا فردية.

وظائف دورية

وظيفة Fيسمى دوري إذا كان هناك رقم مثل هذا لأي xمن مجال تعريف المساواة و (س) = و (س- T) = و (س + T). تيهي فترة الوظيفة.

كل وظيفة دورية لها عدد لا حصر له من الفترات. في الممارسة العملية ، عادة ما يتم النظر في أصغر فترة إيجابية.

تتكرر قيم الوظيفة الدورية بعد فاصل زمني يساوي الفترة. يستخدم هذا عند رسم الرسوم البيانية.

صفحة 1
الدرس 3

"نطاق الوظيفة"
الأهداف: - تطبيق مفهوم مجموعة القيم على حل مشكلة معينة.

حل المشكلات النموذجية.

لعدة سنوات ، ظهرت المشكلات بانتظام في الاختبارات التي يُطلب فيها الاختيار من بين مجموعة معينة من الوظائف أولئك الذين تفي مجموعات قيمهم بالشروط المعلنة.

دعونا نفكر في مثل هذه المهام.

1. 
   تحديث المعرفة.

يتم إجراؤه في شكل حوار مع الطلاب.

ماذا نعني بمجموعة قيم الوظيفة؟

ما هي مجموعة قيم الدالة؟

• 
  من أي بيانات يمكننا إيجاد مجموعة قيم الوظيفة؟ (حسب التدوين التحليلي للدالة أو الرسم البياني الخاص بها)

- باستخدام الشكل ، أوجد مساحة قيم الدالة من الرسوم البيانية.

(سم واجبات الاستخدام، الجزء أ)

• 
  ما هي قيم الدالة التي نعرفها؟ (يتم سرد الوظائف الرئيسية مع كتابتها على السبورة ؛ لكل وظيفة ، يتم تدوين مجموعة القيم الخاصة بها). نتيجة لذلك ، على السبورة وفي دفاتر الطلاب

وظيفة	قيم كثيرة
ذ = x 2 ذ = x 3 ص =| x| ص =	ه ( ذ) = ه ( ذ) = [- 1, 1] ه ( ذ) = (– ∞, + ∞) ه ( ذ) = (– ∞, + ∞) ه ( ذ) = (– ∞, + ∞) ه ( ذ) = (0, + ∞)

• 
  هل يمكننا ، باستخدام هذه المعرفة ، العثور على الفور على مجموعات قيم الوظائف المكتوبة على السبورة؟ (انظر الجدول 2).
• 
  ما الذي يمكن أن يساعد في الإجابة على هذا السؤال؟ (الرسوم البيانية لهذه الوظائف).
• 
  كيف ترسم الوظيفة الأولى؟ (اخفض القطع المكافئ 4 وحدات لأسفل).

وبالمثل ، نتحدث عن كل وظيفة من الجدول.

وظيفة	قيم كثيرة
ذ = x 2 – 4	ه ( ذ) = [-4, + ∞)
ذ = + 5	ه ( ذ) =
ذ = - 5cos x	ه ( ذ) = [- 5, 5]
ص = TG ( x + / 6) – 1	ه ( ذ) = (– ∞, + ∞)
ص =الخطيئة ( x + / 3) – 2	ه ( ذ) = [- 3, - 1]
ص =| x – 1 | + 3	ه ( ذ) =
ص =| ctg x|	ه ( ذ) =
ذ = = | كوس (س +  / 4) |	ه ( ذ) =
ص =(س- 5) 2 + 3	ه ( ذ) = . ابحث عن مجموعة قيم الوظيفة: . إدخال خوارزمية لحل مسائل إيجاد مجموعة قيم الدوال المثلثية. دعونا نرى كيف يمكننا تطبيق خبرتنا على المهام المختلفة المدرجة في خيارات اختبار واحد. 1. إيجاد قيم الوظائف لقيمة معينة من الوسيطة. مثال.أوجد قيمة الدالة y = 2 كوس(π / 2 + / 4 ) – 1, لو س = -π / 2. حل. ذ(-π / 2) = 2 كوس(- π / 2 - π / 4 )- 1= 2 كوس(π / 2 + / 4 )- 1 = - 2 الخطيئةπ / 4-1 = - 2 – 1 = = – – 1. 2. إيجاد مدى الدوال المثلثية حل. 1≤ الخطيئةX≤ 1 2 ≤ 2 الخطيئةX≤ 2 9 ≤ 11+2الخطيئةX≤ 13 3 ≤ +2∙ الخطيئةس ≤ ، أي. ه (ص) =. دعونا نكتب القيم الصحيحة للدالة في الفترة. هذا الرقم هو 3. الجواب: 3. أوجد مجموعة قيم الدالة في= الخطيئة 2 X+ 6 بوصة X + 10. ابحث عن مجموعة قيم الوظيفة: في = الخطيئة 2 X - 6 الخطيئة x + 8 . (على المرء) حل. في= الخطيئة 2 X- 2 3 الخطيئةx + 3 2 - 3 2 + 8, في= (الخطيئةX- 3) 2 -1. ه ( الخطيئةX) = [-1;1]; ه ( الخطيئةX -3) = [-4;-2]; ه ( الخطيئةX -3) 2 = ; ه ( في) = . إجابة: . أوجد أصغر قيمة للدالة في= cos 2 x+ 2sin x – 2. حل. هل يمكننا إيجاد مجموعة من القيم لهذه الدالة؟ (لا.) ما الذي يجب إتمامه؟ (تم تقليله إلى وظيفة واحدة.) كيف افعلها؟ (استخدم الصيغة cos 2 x= 1-sin 2 x.) لذا، في= 1-sin 2 x+ 2sin x –2, ذ= -sin 2 x+ 2sin x –1, في= - (الخطيئة x –1) 2 . حسنًا ، يمكننا الآن إيجاد مجموعة من القيم واختيار أصغرها. 1 ≤ الخطيئة x ≤ 1, 2 ≤ الخطيئة x – 1 ≤ 0, 0 ≤ (الخطيئة x – 1) 2 ≤ 4, 4 ≤ - (الخطيئة x -1) 2 ≤ 0. إذن ، أصغر قيمة للدالة في يؤجر= -4. الجواب: -4. أوجد حاصل ضرب أكبر وأصغر قيم للدالة ص = الخطيئة 2 x+ كوس x + 1,5. حل. في= 1-cos 2 x+ كوس x + 1,5, في= -cos 2 x+ 2 ∙ 0.5 cos x - 0,25 + 2,75, في= - (كوس x- 0,5) 2 + 2,75. E (كوس x) = [-1;1], E (كوس x – 0,5) = [-1,5;0,5], E (كوس x – 0,5) 2 = , ه (- (كوس x-0,5) 2) = [-2,25;0], ه ( في) = . أكبر قيمة للدالة في نيب= 2.75 ؛ أصغر قيمة في يؤجر= 0.5. لنجد حاصل ضرب أكبر وأصغر قيمة للدالة: في نيب ∙في يؤجر = 0,5∙2,75 = 1,375. الجواب: 1.375. حل. دعنا نعيد كتابة الدالة بالشكل في =, في = , دعونا الآن نجد مجموعة قيم الدالة. ه (الخطيئة x) = [-1, 1], E (6 بوصة x) = [-6, 6], E (6 بوصة x + 1) = [-5, 7], E ((6 بوصة x + 1) 2) = , E (- (6 بوصة x + 1) 2) = [-49, 0], E (- (6 بوصة x + 1) 2 + 64) = , ه ( ذ) = [ , 8]. لنجد مجموع قيم الأعداد الصحيحة للدالة: 4 + 5 + 6 + 7 + 8 = 30. الجواب: 30. حل. 1) إنه Xينتمي إلى الربع الأول. 2) لذلك ، 2 Xتنتمي إلى الربع الثاني. 3) في الربع الثاني ، تقل دالة الجيب وتستمر. وسائل، وظيفة معينة يأخذ كل القيم من قبل 4) احسب هذه القيم: إجابة : . حل. 1) بما أن الجيب يأخذ القيم من -1 إلى 1 ، فإن مجموعة قيم الاختلاف . عندما تضرب في هذا الجزء سوف يذهب إلى الجزء . 2) القوسين هو وظيفة متناقصة ومستمرة بشكل رتيب. ومن ثم ، فإن مجموعة قيم التعبير عبارة عن قطعة . 3) عند ضرب هذه القطعة في نحن نحصل . إجابة: . حل. بما أن الظل القوس هو دالة متزايدة ، إذن . 2) عند الزيادة Xمن قبل الحجة 2 Xيزيد من قبل . نظرًا لأن الجيب في مثل هذا الفاصل الزمني يزيد ، فإن الوظيفة يأخذ القيم من تصل إلى 1. 3) عند الزيادة من قبل الحجة 2 Xيزيد من قبل . بما أن الجيب ينخفض ​​في مثل هذا الفاصل ، فإن الوظيفة يأخذ القيم من تصل إلى 1. 4) باستخدام الصيغة التي تعبر عن الجيب بدلالة مماس نصف الزاوية ، نجد ذلك . ومن ثم ، فإن مجموعة القيم المطلوبة هي اتحاد القطع و ، هذا هو الجزء . إجابة: . تستخدم هذه التقنية (مقدمة للزاوية المساعدة) للعثور على مجموعة قيم وظائف النموذج في= a sin x + b cos xأو في= خطيئة (رx) + bcos (رخ). أوجد مجموعة قيم الدالة ص \ u003d 15 sin 2x + 20 cos 2x. حل. لنجد القيمة = = 25. دعونا نحول التعبير 15 sin 2x + 20 cos 2x = 25 ( ) = 25 () = 25 خطيئة (2x + ) ، حيث cos = الخطيئة =. مجموعة قيم الوظيفة y \ u003d sin (2x + ): -1 الخطيئة (2x + ) 1. ثم مجموعة قيم الوظيفة الأصلية -25 25 خطيئة (2x + ) 25. إجابة: [-25; 25]. 3. مهام لإيجاد أكبر وأصغر قيم للدالة في الفترة الزمنية. أوجد أكبر وأصغر قيمة للدالة في= ctg Xعلى المقطع [/ 4 ؛ π / 2]. حل. وظيفة في= ctg Xيتناقص على المقطع [/ 4 ؛ π / 2] ، لذلك ستأخذ الدالة أصغر قيمة عند س =π / 2 أي في(π / 2) = сtg π / 2 = 0 ؛ وأكبر قيمة عند س =π / 4 أي في(π / 4) = сtg π / 4 = 1. الجواب: 1 ، 0. . حل. منفصلة في المساواة الجزء الكامل: . ويترتب على ذلك أن الرسم البياني للدالة f (x) هو إما قطع زائد (а ≠ 0) أو خط مستقيم بدون نقطة. علاوة على ذلك ، إذا أ ؛ 2 أ) و (2 أ ؛ ) وإذا كانت a> 0 ، تزداد بشكل رتيب على هذه الأشعة. إذا كان a \ u003d 0 ، ثم f (x) \ u003d -2 على كامل مجال التعريف x ≠ 0. لذلك ، من الواضح أن القيم المرغوبة للمعلمة لا تساوي الصفر. نظرًا لأننا مهتمون فقط بقيم الوظيفة في المقطع [-1 ؛ 1] ، ثم يتم تحديد تصنيف المواقف من خلال حقيقة أن الخط المقارب x = 2a من القطع الزائد (a ≠ 0) يقع بالنسبة إلى هذا المقطع. الحالة 1. جميع نقاط الفاصل الزمني [-1 ؛ 1] على يمين الخط المقارب العمودي x = 2a ، أي عندما 2a الحالة 2. يتقاطع الخط المقارب العمودي مع الفاصل الزمني [-1 ؛ 1] ، وتنخفض الوظيفة (كما في الحالة 1) ، أي متى الحالة 3. يتقاطع الخط المقارب العمودي مع الفاصل الزمني [-1 ؛ 1] والدالة تتزايد ، أي -1 . الحالة 4. جميع نقاط الفاصل الزمني [-1 ؛ 1] على يسار الخط المقارب العمودي ، أي 1 أ>. والثانية الاستقبال 4 . التعبير عن x بدلالة y. (إيجاد مجال الدالة العكسية) الاستقبال 5.تبسيط الصيغة تحديد دالة كسرية كسرية الاستقبال 6.إيجاد مجموعة قيم الدوال التربيعية (بإيجاد رأس القطع المكافئ وتحديد طبيعة سلوك فروعها). الاستقبال 7.إدخال زاوية مساعدة لإيجاد مجموعة قيم بعض الدوال المثلثية. صفحة 1 اقرأ أيضا: أداء المحاسبة المركزية التخصيم كمصدر لتمويل المشروع أعلى