Paralelogrami dhe zona e tij. Ne llogarisim shumën e këndeve dhe sipërfaqen e një paralelogrami: vetitë dhe shenjat. Karakteristikat e qosheve ngjitur

Zona paralelograme

Teorema 1

Sipërfaqja e një paralelogrami përcaktohet si prodhimi i gjatësisë së anës së tij shumëfishuar me lartësinë e tërhequr drejt tij.

ku $a$ është ana e paralelogramit, $h$ është lartësia e tërhequr në këtë anë.

Dëshmi.

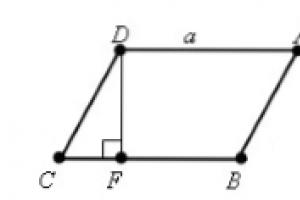
Le të na jepet një paralelogram $ABCD$ me $AD=BC=a$. Le të vizatojmë lartësitë $DF$ dhe $AE$ (Fig. 1).

Foto 1.

Është e qartë se figura $FDAE$ është një drejtkëndësh.

\[\këndi BAE=(90)^0-\këndi A,\ \] \[\këndi CDF=\këndi D-(90)^0=(180)^0-\këndi A-(90)^0 =(90)^0-\këndi A=\këndi BAE\]

Prandaj, meqenëse $CD=AB,\ DF=AE=h$, $\trekëndësh BAE=\trekëndësh CDF$, nga $I$ testi i barazisë së trekëndëshit. Pastaj

Pra, sipas teoremës së zonës drejtkëndëshe:

Teorema është vërtetuar.

Teorema 2

Sipërfaqja e një paralelogrami përcaktohet si prodhimi i gjatësisë së anëve të tij ngjitur me sinusin e këndit midis këtyre anëve.

Matematikisht, kjo mund të shkruhet si më poshtë

ku $a,\ b$ janë brinjët e paralelogramit, $\alfa $ është këndi ndërmjet tyre.

Dëshmi.

Le të na jepet një paralelogram $ABCD$ me $BC=a,\ CD=b,\ \kënd C=\alfa $. Vizatoni lartësinë $DF=h$ (Fig. 2).

Figura 2.

Nga përkufizimi i sinusit, ne marrim

Prandaj

Prandaj, nga teorema $1$:

Teorema është vërtetuar.

Sipërfaqja e një trekëndëshi

Teorema 3

Sipërfaqja e një trekëndëshi përcaktohet si gjysma e produktit të gjatësisë së anës së tij dhe lartësisë së tërhequr drejt tij.

Matematikisht, kjo mund të shkruhet si më poshtë

ku $a$ është brinja e trekëndëshit, $h$ është lartësia e tërhequr në këtë anë.

Dëshmi.

Figura 3

Pra nga teorema $1$:

Teorema është vërtetuar.

Teorema 4

Sipërfaqja e një trekëndëshi përcaktohet si gjysma e produktit të gjatësisë së anëve të tij ngjitur me sinusin e këndit midis këtyre anëve.

Matematikisht, kjo mund të shkruhet si më poshtë

ku $a,\ b$ janë brinjët e trekëndëshit, $\alpha $ është këndi ndërmjet tyre.

Dëshmi.

Le të na jepet një trekëndësh $ABC$ me $AB=a$. Vizatoni lartësinë $CH=h$. Le ta ndërtojmë deri në paralelogramin $ABCD$ (Fig. 3).

Natyrisht, $\trekëndësh ACB=\trekëndësh CDB$ nga $I$. Pastaj

Pra nga teorema $1$:

Teorema është vërtetuar.

Zona e trapezit

Teorema 5

Sipërfaqja e një trapezi përcaktohet si gjysma e produktit të shumës së gjatësive të bazave të tij me lartësinë e tij.

Matematikisht, kjo mund të shkruhet si më poshtë

Dëshmi.

Le të na jepet një trapez $ABCK$, ku $AK=a,\ BC=b$. Le të vizatojmë lartësitë $BM=h$ dhe $KP=h$ në të, si dhe diagonalen $BK$ (Fig. 4).

Figura 4

Nga teorema $3$, marrim

Teorema është vërtetuar.

Shembull i detyrës

Shembulli 1

Gjeni sipërfaqen e një trekëndëshi barabrinjës nëse gjatësia e brinjës së tij është $a.$

Zgjidhje.

Meqenëse trekëndëshi është barabrinjës, të gjitha këndet e tij janë të barabarta me $(60)^0$.

Pastaj, nga teorema $4$, ne kemi

Përgjigje:$\frac(a^2\sqrt(3))(4)$.

Vini re se rezultati i këtij problemi mund të përdoret për të gjetur sipërfaqen e çdo trekëndëshi barabrinjës me një anë të caktuar.

Ashtu si në gjeometrinë Euklidiane, pika dhe vija e drejtë janë elementet kryesore të teorisë së planeve, kështu që paralelogrami është një nga figurat kryesore të katërkëndëshave konveks. Prej tij, si fijet nga një top, rrjedhin konceptet e "drejtkëndëshit", "katrorit", "rombit" dhe sasive të tjera gjeometrike.

Në kontakt me

Përkufizimi i një paralelogrami

katërkëndësh konveks, i përbërë nga segmente, secila palë e të cilave është paralele, në gjeometri njihet si paralelogram.

Si duket një paralelogram klasik është një katërkëndësh ABCD. Brinjët quhen baza (AB, BC, CD dhe AD), pingulja e tërhequr nga çdo kulm në anën e kundërt të kësaj kulme quhet lartësi (BE dhe BF), drejtëzat AC dhe BD janë diagonalet.

Kujdes! Sheshi, rombi dhe drejtkëndëshi janë raste të veçanta të paralelogramit.

Anët dhe këndet: karakteristikat e raportit

Karakteristikat kryesore, në përgjithësi, paracaktuar nga vetë emërtimi, vërtetohen me teoremë. Këto karakteristika janë si më poshtë:

1. Anët që janë të kundërta janë identike në çifte.
2. Këndet që janë përballë njëri-tjetrit janë të barabartë në çifte.

Vërtetim: merrni parasysh ∆ABC dhe ∆ADC, të cilat fitohen duke pjesëtuar katërkëndëshin ABCD me drejtëzën AC. ∠BCA=∠CAD dhe ∠BAC=∠ACD, meqenëse AC është e përbashkët për ta (kënde vertikale për BC||AD dhe AB||CD, përkatësisht). Nga kjo rrjedh: ∆ABC = ∆ADC (kriteri i dytë për barazinë e trekëndëshave).

Segmentet AB dhe BC në ∆ABC korrespondojnë në çift me linjat CD dhe AD në ∆ADC, që do të thotë se ato janë identike: AB = CD, BC = AD. Kështu, ∠B korrespondon me ∠D dhe ato janë të barabarta. Meqenëse ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, të cilat janë gjithashtu identike në çifte, atëherë ∠A = ∠C. Prona eshte e vertetuar.

Karakteristikat e diagonaleve të figurës

Karakteristika kryesore këto drejtëza paralelograme: pika e prerjes i përgjysmon.

Vërtetim: le të jetë m. E pika e prerjes së diagonaleve AC dhe BD të figurës ABCD. Ata formojnë dy trekëndësha proporcionalë - ∆ABE dhe ∆CDE.

AB=CD meqenëse janë të kundërta. Sipas rreshtave dhe sekanteve, ∠ABE = ∠CDE dhe ∠BAE = ∠DCE.

Sipas shenjës së dytë të barazisë, ∆ABE = ∆CDE. Kjo do të thotë se elementët ∆ABE dhe ∆CDE janë: AE = CE, BE = DE dhe, për më tepër, janë pjesë proporcionale të AC dhe BD. Prona eshte e vertetuar.

Karakteristikat e qosheve ngjitur

Në anët ngjitur, shuma e këndeve është 180°, pasi ato shtrihen në të njëjtën anë të drejtëzave paralele dhe sekantit. Për katërkëndëshin ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Karakteristikat e përgjysmimit:

1. , të rënë në njërën anë, janë pingul;
2. kulmet e kundërta kanë përgjysmues paralelë;
3. trekëndëshi i përftuar me vizatimin e përgjysmuesit do të jetë dykëndësh.

Përcaktimi i veçorive karakteristike të një paralelogrami me teoremë

Veçoritë e kësaj figure rrjedhin nga teorema e saj kryesore, e cila thotë si më poshtë: katërkëndëshi konsiderohet paralelogram në rast se diagonalet e tij kryqëzohen, dhe kjo pikë i ndan ato në segmente të barabarta.

Vërtetim: Le të priten drejtëzat AC dhe BD të katërkëndëshit ABCD në t. E. Meqenëse ∠AED = ∠BEC, dhe AE+CE=AC BE+DE=BD, atëherë ∆AED = ∆BEC (me shenjën e parë të barazisë së trekëndëshave). Kjo është, ∠EAD = ∠ECB. Ato janë gjithashtu këndet e brendshme të kryqëzimit të AC sekante për linjat AD dhe BC. Kështu, sipas përkufizimit të paralelizmit - AD || para Krishtit. Një veti e ngjashme e linjave BC dhe CD rrjedh gjithashtu. Teorema është vërtetuar.

Llogaritja e sipërfaqes së një figure

Zona e kësaj figure gjendet në disa mënyra një nga më të thjeshtat: shumëzimi i lartësisë dhe bazës në të cilën është tërhequr.

Vërtetim: Vizatoni pingulet BE dhe CF nga kulmet B dhe C. ∆ABE dhe ∆DCF janë të barabarta pasi AB = CD dhe BE = CF. ABCD është e barabartë me drejtkëndëshin EBCF, pasi ato gjithashtu përbëhen nga figura proporcionale: S ABE dhe S EBCD, si dhe S DCF dhe S EBCD. Nga kjo rrjedh se zona e kësaj figure gjeometrike është e njëjtë me atë të një drejtkëndëshi:

S ABCD = S EBCF = BE×BC=BE×AD.

Për të përcaktuar formulën e përgjithshme për sipërfaqen e një paralelogrami, shënojmë lartësinë si hb, dhe anash b. Përkatësisht:

Mënyra të tjera për të gjetur zonën

Llogaritjet e sipërfaqes nëpër brinjët e paralelogramit dhe këndit, që ata formojnë, është metoda e dytë e njohur.

,

Spr-ma - zonë;

a dhe b janë anët e tij

α - këndi ndërmjet segmenteve a dhe b.

Kjo metodë praktikisht bazohet në të parën, por në rast se nuk dihet. gjithmonë pret një trekëndësh kënddrejtë, parametrat e të cilit gjenden me identitete trigonometrike, d.m.th. Duke transformuar raportin, marrim . Në ekuacionin e metodës së parë, ne zëvendësojmë lartësinë me këtë produkt dhe marrim një provë të vlefshmërisë së kësaj formule.

Përmes diagonaleve të një paralelogrami dhe një këndi, që krijojnë kur kryqëzohen, mund të gjesh edhe zonën.

Vërtetim: AC dhe BD duke kryqëzuar formojnë katër trekëndësha: ABE, BEC, CDE dhe AED. Shuma e tyre është e barabartë me sipërfaqen e këtij katërkëndëshi.

Zona e secilës prej këtyre ∆ mund të gjendet nga shprehja , ku a=BE, b=AE, ∠γ =∠AEB. Meqenëse , atëherë një vlerë e vetme e sinusit përdoret në llogaritjet. Kjo eshte . Meqenëse AE+CE=AC= d 1 dhe BE+DE=BD= d 2, formula e zonës zvogëlohet në:

.

Zbatim në algjebër vektoriale

Veçoritë e pjesëve përbërëse të këtij katërkëndëshi kanë gjetur zbatim në algjebër vektoriale, përkatësisht: shtimi i dy vektorëve. Rregulli i paralelogramit thotë se nëse jepen vektorëDheJojanë kolineare, atëherë shuma e tyre do të jetë e barabartë me diagonalen e kësaj figure, bazat e së cilës i përgjigjen këtyre vektorëve.

Dëshmi: nga një fillim i zgjedhur në mënyrë arbitrare - d.m.th. - ndërtojmë vektorë dhe . Më pas, ndërtojmë një paralelogram OASV, ku segmentet OA dhe OB janë anët. Kështu, OS shtrihet në vektor ose shumë.

Formulat për llogaritjen e parametrave të një paralelogrami

Identiteti jepet në kushtet e mëposhtme:

1. a dhe b, α - brinjët dhe këndi ndërmjet tyre;
2. d 1 dhe d 2 , γ - diagonalet dhe në pikën e kryqëzimit të tyre;
3. h a dhe h b - lartësitë e ulura në anët a dhe b;

Parametri	Formula
Gjetja e anëve
përgjatë diagonaleve dhe kosinusit të këndit ndërmjet tyre
diagonalisht dhe anash
përmes lartësisë dhe kulmit të kundërt
Gjetja e gjatësisë së diagonaleve
në anët dhe madhësia e majës ndërmjet tyre
përgjatë anëve dhe njërës nga diagonalet	 konkluzioni Paralelogrami, si një nga figurat kryesore të gjeometrisë, përdoret në jetë, për shembull, në ndërtim kur llogaritet sipërfaqja e një vendi ose matje të tjera. Prandaj, njohuritë për veçoritë dalluese dhe metodat për llogaritjen e parametrave të ndryshëm të tij mund të jenë të dobishme në çdo kohë të jetës.

Gjatë zgjidhjes së problemeve në këtë temë, përveç vetitë themelore paralelogrami dhe formulat përkatëse, mund të mbani mend dhe zbatoni sa vijon:

1. Përgjysmuesja e këndit të brendshëm të një paralelogrami pret një trekëndësh dykëndësh prej tij
2. Përgjysmuesit e këndeve të brendshëm ngjitur me njërën nga brinjët e një paralelogrami janë reciprokisht pingul
3. Përgjysmues që vijnë nga kënde të brendshme të kundërta të një paralelogrami, paralel me njëri-tjetrin ose shtrihen në një vijë të drejtë
4. Shuma e katrorëve të diagonaleve të një paralelogrami është e barabartë me shumën e katrorëve të brinjëve të tij
5. Sipërfaqja e një paralelogrami është gjysma e prodhimit të diagonaleve me sinusin e këndit ndërmjet tyre.

Le të shqyrtojmë detyrat në zgjidhjen e të cilave përdoren këto veti.

Detyra 1.

Përgjysmuesja e këndit C të paralelogramit ABCD kryqëzon anën AD në pikën M dhe vazhdimin e brinjës AB përtej pikës A në pikën E. Gjeni perimetrin e paralelogramit nëse AE \u003d 4, DM \u003d 3.

Zgjidhje.

1. Trekëndëshi CMD isosceles. (Prona 1). Prandaj, CD = MD = 3 cm.

2. Trekëndëshi EAM është dykëndësh.
Prandaj, AE = AM = 4 cm.

3. AD = AM + MD = 7 cm.

4. Perimetri ABCD = 20 cm.

Përgjigju. 20 cm

Detyra 2.

Diagonalet vizatohen në një katërkëndësh konveks ABCD. Dihet se sipërfaqet e trekëndëshave ABD, ACD, BCD janë të barabarta. Vërtetoni se katërkëndëshi i dhënë është paralelogram.

Zgjidhje.

1. Le të jetë BE lartësia e trekëndëshit ABD, CF lartësia e trekëndëshit ACD. Meqenëse, sipas kushtit të problemit, sipërfaqet e trekëndëshave janë të barabarta dhe kanë një bazë të përbashkët AD, atëherë lartësitë e këtyre trekëndëshave janë të barabarta. BE = CF.

2. BE, CF janë pingul me AD. Pikat B dhe C ndodhen në të njëjtën anë të vijës AD. BE = CF. Prandaj, vija BC || pas Krishtit. (*)

3. Le të jetë AL lartësia e trekëndëshit ACD, BK lartësia e trekëndëshit BCD. Meqenëse, sipas kushtit të problemës, sipërfaqet e trekëndëshave janë të barabarta dhe kanë një bazë të përbashkët CD, atëherë lartësitë e këtyre trekëndëshave janë të barabarta. AL = BK.

4. AL dhe BK janë pingul me CD. Pikat B dhe A janë të vendosura në të njëjtën anë të vijës së drejtë CD. AL = BK. Prandaj, rreshti AB || CD (**)

5. Kushtet (*), (**) nënkuptojnë se ABCD është një paralelogram.

Përgjigju. E provuar. ABCD është një paralelogram.

Detyra 3.

Në faqet BC dhe CD të paralelogramit ABCD, janë shënuar përkatësisht pikat M dhe H, në mënyrë që segmentet BM dhe HD të priten në pikën O;<ВМD = 95 о,