Paralelogram i njegova površina. Izračunavamo zbir uglova i površine paralelograma: svojstva i znakovi. Karakteristike susjednih uglova

Područje paralelograma

Teorema 1

Površina paralelograma definirana je kao umnožak dužine njegove stranice puta visine koja mu je povučena.

gdje je $a$ stranica paralelograma, $h$ je visina povučena na ovu stranu.

Dokaz.

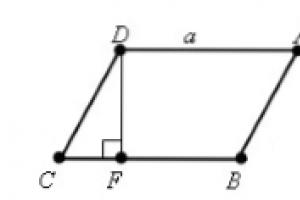
Neka nam je dat paralelogram $ABCD$ sa $AD=BC=a$. Nacrtajmo visine $DF$ i $AE$ (slika 1).

Slika 1.

Očigledno je da je figura $FDAE$ pravougaonik.

\[\ugao BAE=(90)^0-\ugao A,\ \] \[\ugao CDF=\ugao D-(90)^0=(180)^0-\ugao A-(90)^0=(90)^0-\ugao A=\ugao BAE\]

Stoga, pošto $CD=AB,\ DF=AE=h$, $\trougao BAE=\trougao CDF$, po $I$ test jednakosti trougla. Onda

Dakle, prema teoremi o površini pravougaonika:

Teorema je dokazana.

Teorema 2

Površina paralelograma definirana je kao proizvod dužine njegovih susjednih stranica puta sinusa ugla između tih stranica.

Matematički, ovo se može napisati na sljedeći način

gdje su $a,\ b$ stranice paralelograma, $\alpha $ je ugao između njih.

Dokaz.

Neka nam je dat paralelogram $ABCD$ sa $BC=a,\ CD=b,\ \ugao C=\alpha $. Nacrtajte visinu $DF=h$ (slika 2).

Slika 2.

Po definiciji sinusa, dobijamo

Dakle

Dakle, prema teoremi $1$:

Teorema je dokazana.

Površina trougla

Teorema 3

Površina trokuta definirana je kao polovina umnožaka dužine njegove stranice i visine koja mu je povučena.

Matematički, ovo se može napisati na sljedeći način

gdje je $a$ stranica trougla, $h$ je visina povučena na ovu stranu.

Dokaz.

Slika 3

Dakle, prema teoremi $1$:

Teorema je dokazana.

Teorema 4

Površina trokuta je definirana kao polovina umnožaka dužine njegovih susjednih stranica puta sinusa ugla između tih stranica.

Matematički, ovo se može napisati na sljedeći način

gdje su $a,\ b$ stranice trougla, $\alpha $ je ugao između njih.

Dokaz.

Neka nam je dat trougao $ABC$ sa $AB=a$. Nacrtajte visinu $CH=h$. Izgradimo ga do paralelograma $ABCD$ (slika 3).

Očigledno, $\trougao ACB=\trougao CDB$ prema $I$. Onda

Dakle, prema teoremi $1$:

Teorema je dokazana.

Područje trapeza

Teorema 5

Površina trapeza definirana je kao polovina umnožaka zbroja dužina njegovih osnova puta njegove visine.

Matematički, ovo se može napisati na sljedeći način

Dokaz.

Neka nam je dat trapez $ABCK$, gdje je $AK=a,\ BC=b$. Nacrtajmo u njemu visine $BM=h$ i $KP=h$, kao i dijagonalu $BK$ (slika 4).

Slika 4

Prema teoremi $3$, dobijamo

Teorema je dokazana.

Primjer zadatka

Primjer 1

Nađite površinu jednakostraničnog trougla ako je dužina njegove stranice $a.$

Rješenje.

Pošto je trokut jednakostraničan, svi njegovi uglovi jednaki su $(60)^0$.

Zatim, prema teoremi $4$, imamo

odgovor:$\frac(a^2\sqrt(3))(4)$.

Imajte na umu da se rezultat ovog problema može koristiti za pronalaženje površine bilo kojeg jednakostraničnog trokuta sa datom stranom.

Kao iu euklidskoj geometriji, tačka i prava linija su glavni elementi teorije ravni, pa je paralelogram jedna od ključnih figura konveksnih četvorouglova. Iz njega, poput niti iz lopte, teku koncepti "pravougaonika", "kvadrata", "romba" i drugih geometrijskih veličina.

U kontaktu sa

Definicija paralelograma

konveksan četvorougao, koji se sastoji od segmenata, od kojih je svaki par paralelan, poznat je u geometriji kao paralelogram.

Kako izgleda klasični paralelogram je četverougao ABCD. Stranice se nazivaju osnovicama (AB, BC, CD i AD), okomice povučene iz bilo kojeg vrha na suprotnu stranu ovog vrha nazivaju se visinom (BE i BF), prave AC i BD su dijagonale.

Pažnja! Kvadrat, romb i pravougaonik su posebni slučajevi paralelograma.

Stranice i uglovi: karakteristike omjera

Ključna svojstva, uglavnom, unaprijed određeno samom oznakom, oni su dokazani teoremom. Ove karakteristike su sljedeće:

1. Strane koje su suprotne su identične u parovima.
2. Uglovi koji su suprotni jedan drugom jednaki su u parovima.

Dokaz: razmotrite ∆ABC i ∆ADC, koji se dobijaju dijeljenjem četverougla ABCD pravom AC. ∠BCA=∠CAD i ∠BAC=∠ACD, pošto im je AC zajednički (vertikalni uglovi za BC||AD i AB||CD, respektivno). Iz ovoga slijedi: ∆ABC = ∆ADC (drugi kriterij jednakosti trouglova).

Segmenti AB i BC u ∆ABC odgovaraju u parovima linijama CD i AD u ∆ADC, što znači da su identični: AB = CD, BC = AD. Dakle, ∠B odgovara ∠D i oni su jednaki. Pošto su ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, koji su takođe identični u parovima, onda je ∠A = ∠C. Imovina je dokazana.

Karakteristike dijagonala figure

Glavna karakteristika ove paralelogramske prave: tačka preseka ih deli na pola.

Dokaz: neka je m. E presjek dijagonala AC i BD figure ABCD. Oni formiraju dva srazmerna trougla - ∆ABE i ∆CDE.

AB=CD jer su suprotne. Prema linijama i sekantima, ∠ABE = ∠CDE i ∠BAE = ∠DCE.

Prema drugom znaku jednakosti, ∆ABE = ∆CDE. To znači da su elementi ∆ABE i ∆CDE: AE = CE, BE = DE i, štaviše, oni su srazmjerni dijelovi AC i BD. Imovina je dokazana.

Karakteristike susjednih uglova

Na susjednim stranama zbir uglova je 180°, budući da leže na istoj strani paralelnih pravih i sekanse. Za četvorougao ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Svojstva simetrale:

1. , spušteni na jednu stranu, su okomiti;
2. suprotni vrhovi imaju paralelne simetrale;
3. trokut dobijen povlačenjem simetrale bit će jednakokračan.

Određivanje karakteristika paralelograma teoremom

Karakteristike ove figure proizlaze iz njene glavne teoreme, koja glasi: četvorougao se smatra paralelogramom u slučaju da se njegove dijagonale sijeku, a ova tačka ih dijeli na jednake segmente.

Dokaz: Neka se prave AC i BD četverougla ABCD sijeku u t. E. Kako je ∠AED = ∠BEC, a AE+CE=AC BE+DE=BD, onda je ∆AED = ∆BEC (prema prvom znaku jednakosti trouglova). To jest, ∠EAD = ∠ECB. Oni su takođe unutrašnji uglovi ukrštanja sekante AC za prave AD i BC. Dakle, po definiciji paralelizma - AD || BC. Slično svojstvo pravih BC i CD je također izvedeno. Teorema je dokazana.

Izračunavanje površine figure

Područje ove figure nalazi na nekoliko načina jedan od najjednostavnijih: množenje visine i osnove na koju je nacrtana.

Dokaz: Nacrtajte okomite BE i CF iz vrhova B i C. ∆ABE i ∆DCF su jednaki jer su AB = CD i BE = CF. ABCD je jednak pravougaoniku EBCF, jer se i oni sastoje od proporcionalnih figura: S ABE i S EBCD, kao i S DCF i S EBCD. Iz toga slijedi da je površina ove geometrijske figure ista kao i pravokutnika:

S ABCD = S EBCF = BE×BC=BE×AD.

Da bismo odredili opću formulu za površinu paralelograma, označavamo visinu kao hb, i sa strane b. odnosno:

Drugi načini za pronalaženje područja

Proračuni površine kroz stranice paralelograma i ugla, koji oni formiraju, je druga poznata metoda.

,

Spr-ma - područje;

a i b su njegove stranice

α - ugao između segmenata a i b.

Ova metoda je praktično zasnovana na prvoj, ali u slučaju da je nepoznata. uvijek odsijeca pravougaoni trougao čiji se parametri nalaze trigonometrijskim identitetima, tj. Transformirajući omjer, dobijamo . U jednadžbi prve metode zamjenjujemo visinu ovim proizvodom i dobivamo dokaz valjanosti ove formule.

Kroz dijagonale paralelograma i ugla, koje stvaraju kada se ukrštaju, također možete pronaći područje.

Dokaz: AC i BD koji se seku formiraju četiri trougla: ABE, BEC, CDE i AED. Njihov zbir je jednak površini ovog četvorougla.

Površina svakog od ovih ∆ može se naći iz izraza , gdje je a=BE, b=AE, ∠γ =∠AEB. Budući da se u proračunima koristi jedna vrijednost sinusa. To je . Budući da AE+CE=AC= d 1 i BE+DE=BD= d 2 , formula površine se svodi na:

.

Primjena u vektorskoj algebri

Karakteristike sastavnih delova ovog četvorougla našle su primenu u vektorskoj algebri, i to: sabiranje dva vektora. Pravilo paralelograma to kaže ako su dati vektoriINesu kolinearni, onda će njihov zbir biti jednak dijagonali ove figure, čije baze odgovaraju ovim vektorima.

Dokaz: sa proizvoljno izabranog početka - tj. - gradimo vektore i . Zatim gradimo paralelogram OASV, gdje su segmenti OA i OB stranice. Dakle, OS leži na vektoru ili zbiru.

Formule za izračunavanje parametara paralelograma

Identiteti se daju pod sledećim uslovima:

1. a i b, α - stranice i ugao između njih;
2. d 1 i d 2 , γ - dijagonale i u tački njihovog preseka;
3. h a i h b - visine spuštene na strane a i b;

Parametar	Formula
Pronalaženje strana
duž dijagonala i kosinusa ugla između njih
dijagonalno i bočno
kroz visinu i suprotni vrh
Pronalaženje dužine dijagonala
na stranama i veličini vrha između njih
duž stranica i jedne od dijagonala	 Zaključak Paralelogram, kao jedna od ključnih figura geometrije, koristi se u životu, na primjer, u građevinarstvu kada se izračunava površina lokacije ili druga mjerenja. Stoga znanje o karakterističnim karakteristikama i metodama za izračunavanje njegovih različitih parametara može biti korisno u bilo kojem trenutku u životu.

Prilikom rješavanja zadataka na ovu temu, pored osnovna svojstva paralelogram i odgovarajuće formule, možete zapamtiti i primijeniti sljedeće:

1. Simetrala unutrašnjeg ugla paralelograma odsiječe od njega jednakokraki trokut
2. Simetrale unutrašnjih uglova susedne jednoj od stranica paralelograma su međusobno okomite
3. Simetrale koje dolaze iz suprotnih unutrašnjih uglova paralelograma, paralelne jedna drugoj ili leže na jednoj pravoj liniji
4. Zbir kvadrata dijagonala paralelograma jednak je zbroju kvadrata njegovih stranica
5. Površina paralelograma je polovina umnožaka dijagonala puta sinusa ugla između njih.

Razmotrimo zadatke u čijem rješavanju se koriste ova svojstva.

Zadatak 1.

Simetrala ugla C paralelograma ABCD siječe stranu AD u tački M i nastavak stranice AB izvan tačke A u tački E. Pronađite perimetar paralelograma ako je AE = 4, DM = 3.

Rješenje.

1. Trougao CMD jednakokračan. (Svojstvo 1). Dakle, CD = MD = 3 cm.

2. Trougao EAM je jednakokračan.
Dakle, AE = AM = 4 cm.

3. AD = AM + MD = 7 cm.

4. Perimetar ABCD = 20 cm.

Odgovori. 20 cm

Zadatak 2.

Dijagonale su nacrtane u konveksnom četvorouglu ABCD. Poznato je da su površine trouglova ABD, ACD, BCD jednake. Dokazati da je dati četverougao paralelogram.

Rješenje.

1. Neka je BE visina trougla ABD, CF visina trougla ACD. Kako su, prema uslovu zadatka, površine trouglova jednake i imaju zajedničku osnovu AD, onda su i visine ovih trouglova jednake. BE = CF.

2. BE, CF su okomite na AD. Tačke B i C nalaze se na istoj strani prave AD. BE = CF. Dakle, pravac BC || AD. (*)

3. Neka je AL visina trougla ACD, BK visina trougla BCD. Kako su, prema uslovu zadatka, površine trouglova jednake i imaju zajedničku osnovu CD, onda su i visine ovih trouglova jednake. AL = BK.

4. AL i BK su okomite na CD. Tačke B i A nalaze se na istoj strani prave CD. AL = BK. Dakle, pravac AB || CD (**)

5. Uslovi (*), (**) impliciraju da je ABCD paralelogram.

Odgovori. Dokazan. ABCD je paralelogram.

Zadatak 3.

Na stranicama BC i CD paralelograma ABCD označene su tačke M i H, tako da se segmenti BM i HD sijeku u tački O;<ВМD = 95 о,