What is the sum of the angles of a convex polygon. Theorem on the sum of the angles of a triangle What is the sum of the angles

In the 8th grade, in geometry lessons at school, students for the first time get acquainted with the concept of a convex polygon. Very soon they will learn that this figure has a very interesting property. No matter how complex it may be, the sum of all the internal and external angles of a convex polygon takes on a strictly defined value. In this article, a tutor in mathematics and physics talks about what the sum of the angles of a convex polygon is.

The sum of the interior angles of a convex polygon

How to prove this formula?

Before proceeding to the proof of this statement, we recall which polygon is called convex. A polygon is called convex if it lies entirely on one side of the line containing any of its sides. For example, the one shown in this picture:

If the polygon does not satisfy the specified condition, then it is called non-convex. For example, like this:

The sum of the interior angles of a convex polygon is , where is the number of sides of the polygon.

The proof of this fact is based on the theorem on the sum of angles in a triangle, well known to all schoolchildren. I am sure that you are familiar with this theorem. The sum of the interior angles of a triangle is .

The idea is to split a convex polygon into multiple triangles. It can be done different ways. Depending on which method we choose, the evidence will be slightly different.

1. Divide a convex polygon into triangles by all possible diagonals drawn from some vertex. It is easy to understand that then our n-gon will be divided into triangles:

Moreover, the sum of all the angles of all the resulting triangles is equal to the sum of the angles of our n-gon. After all, each angle in the resulting triangles is a partial angle in our convex polygon. That is, the required amount is equal to .

2. You can also select a point inside the convex polygon and connect it to all vertices. Then our n-gon will be divided into triangles:

Moreover, the sum of the angles of our polygon in this case will be equal to the sum of all the angles of all these triangles minus the central angle, which is equal to . That is, the desired amount is again equal to .

The sum of the exterior angles of a convex polygon

Let us now ask ourselves the question: “What is the sum of the external angles of a convex polygon?” This question can be answered in the following way. Each outer corner is adjacent to the corresponding inner corner. Therefore it is equal to:

Then the sum of all external angles is . That is, it is equal to .

That is a very funny result. If we lay aside sequentially one after another all the external corners of any convex n-gon, then as a result exactly the entire plane will be filled.

This interesting fact can be illustrated as follows. Let's proportionally reduce all sides of some convex polygon until it merges into a point. After this happens, all the outer corners will be set aside one from the other and thus fill the entire plane.

Interesting fact, isn't it? And there are a lot of such facts in geometry. So learn geometry, dear students!

The material on what the sum of the angles of a convex polygon is equal to was prepared by Sergey Valerievich

The sum of the interior angles of a triangle is 180 0 . This is one of the fundamental axioms of Euclid's geometry. It is this geometry that students study. Geometry is defined as the science that studies the spatial forms of the real world.

What prompted the ancient Greeks to develop geometry? The need to measure fields, meadows - areas of the earth's surface. At the same time, the ancient Greeks accepted that the surface of the Earth is horizontal, flat. With this assumption in mind, Euclid's axioms were created, including the sum of the interior angles of a triangle at 180 0 .

An axiom is a statement that does not require proof. How should this be understood? A wish is expressed that suits a person, and then it is confirmed by illustrations. But everything that is not proven is fiction, something that is not in reality.

Taking earth's surface horizontal, the ancient Greeks automatically assumed the shape of the Earth as flat, but it is different - spherical. There are no horizontal planes and straight lines in nature at all, because gravity bends space. Straight lines and horizontal planes are found only in the brain of the human head.

Therefore, Euclid's geometry, which explains the spatial forms of a fictional world, is a simulacrum - a copy that does not have an original.

One of Euclid's axioms states that the sum of the interior angles of a triangle is 180 0 . In fact, in a real curved space, or on the spherical surface of the Earth, the sum of the interior angles of a triangle is always greater than 180 0 .

We reason like this. Any meridian on the globe intersects with the equator at an angle of 90 0 . To get a triangle, you need to move another meridian away from the meridian. The sum of the angles of the triangle between the meridians and the side of the equator will be 180 0 . But there will still be an angle at the pole. As a result, the sum of all angles and will be more than 180 0.

If the sides intersect at the pole at an angle of 90 0, then the sum of the interior angles of such a triangle will be 270 0. Two meridians intersecting with the equator at right angles in this triangle will be parallel to each other, and at the pole, intersecting with each other at an angle of 90 0, they will become perpendicular. It turns out that two parallel lines on the same plane not only intersect, but can be perpendicular at the pole.

Of course, the sides of such a triangle will not be straight lines, but convex, repeating the spherical shape of the globe. But, just like that real world space.

The geometry of real space, taking into account its curvature in the middle of the XIX century. developed by the German mathematician B. Riemann (1820-1866). But the students are not told about it.

So, the Euclidean geometry, which takes the form of a flat Earth with a horizontal surface, which is not actually the case, is a simulacrum. Nootic - Riemannian geometry that takes into account the curvature of space. The sum of the interior angles of a triangle in it is greater than 180 0 .

Following up on yesterday:

We play with a mosaic for a fairy tale in geometry:

There were triangles. So similar that they are just copies of each other.
They stood side by side in a straight line. And since they were all the same height -
then their tops were on the same level, under the ruler:

Triangles loved to roll and stand on their heads. They climbed to the top row and stood on the corner like acrobats.
And we already know - when they stand with their tops exactly in a line,
then their soles are also lined - because if someone is of the same height, then he is upside down with the same height!

In everything they were the same - and the height was the same, and the soles were one to one,
and slides on the sides - one is steeper, the other is more gentle - the same length
and they have the same slope. Well, just twins! (only in different clothes, each has its own piece of the puzzle).

Where do the triangles have the same sides? Where are the corners?

Triangles stood on the head, stood, and decided to slip off and lie down in the bottom row.
Slipped and slid down like a hill; and the slides are the same!
So they fit exactly between the lower triangles, without gaps, and no one pressed anyone.

We looked around the triangles and noticed an interesting feature.
Wherever their corners met together, all three corners certainly met:
the largest is the "angle-head", the sharpest angle and the third, average angle.
They even tied colored ribbons, so that it would be immediately noticeable where it was.

And it turned out that the three corners of the triangle, if you combine them -
make up one big corner, "open corner" - like the cover of an open book,

______________________O ___________________

That's what it's called: a twisted angle.

Any triangle is like a passport: three angles together are equal to a straight angle.
Someone will knock on you: - knock-knock, I'm a triangle, let me spend the night!
And you to him - Show me the sum of the angles in expanded form!
And it is immediately clear whether this is a real triangle or an impostor.
Failed verification - Turn around one hundred and eighty degrees and go home!

When they say "turn 180 °" it means to turn around backwards and
go in the opposite direction.

The same in more familiar expressions, without "they lived":

Let's make a parallel translation of the triangle ABC along the axis OX
per vector AB equal to the length of the base AB.
Line DF passing through vertices C and C 1 of triangles
parallel to the OX axis, due to the fact that perpendicular to the OX axis
the segments h and h 1 (heights of equal triangles) are equal.
Thus, the base of the triangle A 2 B 2 C 2 is parallel to the base AB
and equal to it in length (because the top C 1 is shifted relative to C by the amount AB).
Triangles A 2 B 2 C 2 and ABC are equal on three sides.
And so the angles ∠A 1 ∠B ∠C 2 , forming a developed angle, are equal to the angles of the triangle ABC.
=> The sum of the angles of a triangle is 180°

With movements - "broadcasts" the so-called proof is shorter and clearer,
on the pieces of the puzzle, even a baby can understand.

But the traditional school:

based on the equality of internal cross-lying angles cut off on parallel lines

valuable in that it gives an idea of ​​why this is so,
Why the sum of the angles of a triangle is equal to the angle?

Because otherwise parallel lines would not have the properties familiar to our world.

Theorems work both ways. From the axiom of parallel lines it follows
equality of crosswise lying and vertical angles, and of them - the sum of the angles of a triangle.

But the opposite is also true: as long as the angles of the triangle are 180 ° - there are parallel lines
(such that through a point not lying on a line it is possible to draw a unique line || given).
If one day a triangle appears in the world, in which the sum of the angles is not equal to the straight angle -
then the parallel ones will cease to be parallel, the whole world will be twisted and skewed.

If stripes with an ornament of triangles are placed one above the other -
you can cover the entire field with a repeating pattern, like a floor with tiles:

you can trace different shapes on such a grid - hexagons, rhombuses,
star polygons and get a variety of parquets

Tiling a plane with parquet is not only an entertaining game, but also an actual mathematical problem:

________________________________________ _______________________-------__________ ________________________________________ ______________
/\__||_/\__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/ \__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\

Since each quadrilateral is a rectangle, square, rhombus, etc.,
can be made up of two triangles,
respectively, the sum of the angles of the quadrilateral: 180° + 180°= 360°

Identical isosceles triangles are folded into squares in different ways.
Small square in 2 parts. Medium of 4. And the largest of the 8.
How many figures in the drawing, consisting of 6 triangles?

Triangle . Acute, obtuse and right triangles.

The legs and the hypotenuse. Isosceles and equilateral triangle.

The sum of the angles of a triangle.

The outer corner of the triangle. Signs of equality of triangles.

Wonderful lines and points in a triangle: heights, medians,

bisectors, median e perpendiculars, orthocenter,

center of gravity, center of the circumscribed circle, center of the inscribed circle.

Pythagorean theorem. The aspect ratio of an arbitrary triangle.

Triangle is a polygon with three sides (or three corners). The sides of a triangle are often denoted by small letters, which correspond to capital letters denoting opposite vertices.

If all three angles are acute ( fig. 20), then this acute triangle . If one of the corners is right(C, fig.21), that is right triangle; sidesa , bforming a right angle are called legs; sidecopposite the right angle is called hypotenuse. If one of obtuse angles ( B, fig.22), that is obtuse triangle.


Triangle ABC (Fig. 23) - isosceles, If two its sides are equala= c); these equal sides are called lateral, the third party is called basis triangle. Triangle ABC (Fig. 24) - equilateral, If All its sides are equala = b = c). In general ( a ≠ b ≠ c) we have scalene triangle .

Basic properties of triangles. In any triangle:

1. There is a larger angle opposite the larger side, and vice versa.

2. Equal angles lie opposite equal sides, and vice versa.

In particular, all angles in equilateral triangle are equal.

3. The sum of the angles of a triangle is 180 º .

From the last two properties it follows that each angle in an equilateral

triangle is 60 º.

4. Continuing one of the sides of the triangle (AC, fig. 25), we get external

angle BCD . The exterior angle of a triangle is equal to the sum of the interior angles,

not related to it :BCD=A+B.

5. Any side of a triangle is less than the sum of the other two sides and more

their differences (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Signs of equality of triangles.

Triangles are congruent if they are respectively equal:

a ) two sides and the angle between them;

b ) two corners and the side adjacent to them;

c) three sides.

Signs of equality of right triangles.

Two rectangular triangles are congruent if one of the following conditions is true:

1) their legs are equal;

2) the leg and hypotenuse of one triangle are equal to the leg and hypotenuse of the other;

3) the hypotenuse and the acute angle of one triangle are equal to the hypotenuse and the acute angle of the other;

4) the leg and the adjacent acute angle of one triangle are equal to the leg and the adjacent acute angle of the other;

5) the leg and the opposite acute angle of one triangle are equal to the leg and opposite the acute angle of the other.

Wonderful lines and dots in a triangle.

Height triangle isperpendicular,dropped from any vertex to the opposite side ( or its continuation). This side is calledthe base of the triangle . The three altitudes of a triangle always intersectat one pointcalled orthocenter triangle. The orthocenter of an acute triangle (point O , Fig. 26) is located inside the triangle, andorthocenter of an obtuse triangle (point O , Fig.27) – outside; The orthocenter of a right triangle coincides with the vertex of the right angle.

Median - This line segment , connecting any vertex of a triangle with the midpoint of the opposite side. Three medians of a triangle (AD , BE , CF , fig.28) intersect at one point O , which always lies inside the triangle and being his center of gravity. This point divides each median 2:1 from the top.

Bisector - This bisector segment corner from top to point intersection with the opposite side. Three bisectors of a triangle (AD , BE , CF , fig.29) intersect at one point Oh, always lying inside a triangle And being inscribed circle center(see section "Inscribedand circumscribed polygons).

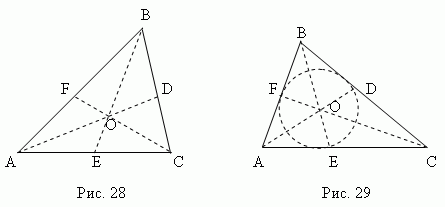
The bisector divides the opposite side into parts proportional to the adjacent sides ; for example, in Fig.29 AE : CE = AB : BC .

Median perpendicular is a perpendicular drawn from the mean segment points (sides). Three perpendicular bisectors of triangle ABC(KO , MO , NO , fig.30 ) intersect at one point O, which is center circumscribed circle (points K , M , N the midpoints of the sides of a triangle ABC).

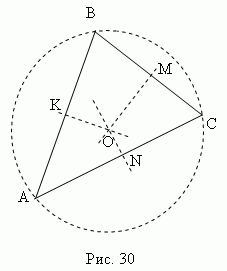
In an acute triangle, this point lies inside the triangle; in obtuse - outside; in a rectangular - in the middle of the hypotenuse. Orthocenter, center of gravity, center of the circumscribed and center of the inscribed circle coincide only in an equilateral triangle.

Pythagorean theorem. In a right triangle, the square of the lengthThe hypotenuse is equal to the sum of the squares of the lengths of the legs.

The proof of the Pythagorean theorem obviously follows from Fig.31. Consider a right triangle ABC with legs a , b and hypotenuse c.

Let's build a square AKMB using the hypotenuse AB as a side. Thenextend the sides of a right triangle ABC so to get a square CDEF , whose side is equal toa + b .Now it is clear that the area of ​​a square CDEF is ( a+b) 2 . On the other hand, this the area is equal to the sum areas four right triangles and square AKMB , that is

c 2 + 4 (ab / 2) = c 2 + 2 ab,

from here,

c 2 + 2 ab= (a+b) 2 ,

and finally we have:

c 2 =a 2 +b 2 .

The aspect ratio of an arbitrary triangle.

In the general case (for an arbitrary triangle) we have:

c 2 =a 2 +b 2 – 2ab· cos c,

where C - angle between sidesa And b .

Proof:

• Triangle ABC is given.
• Draw a line DK through the vertex B parallel to the base AC.
• \angle CBK= \angle C as internal crosswise lying with parallel DK and AC, and secant BC.
• \angle DBA = \angle A internal crosswise lying at DK \parallel AC and secant AB. Angle DBK is straight and equal to
• \angle DBK = \angle DBA + \angle B + \angle CBK
• Since the straight angle is 180 ^\circ , and \angle CBK = \angle C and \angle DBA = \angle A , we get 180 ^\circ = \angle A + \angle B + \angle C.

Theorem proven

Consequences from the theorem on the sum of angles of a triangle:

1. The sum of the acute angles of a right triangle is 90°.
2. In an isosceles right triangle, each acute angle is 45°.
3. In an equilateral triangle, each angle is 60°.
4. In any triangle, either all angles are acute, or two angles are acute, and the third is obtuse or right.
5. An exterior angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.

Triangle exterior angle theorem

An exterior angle of a triangle is equal to the sum of the two remaining angles of the triangle that are not adjacent to that exterior angle.

Proof:

• Triangle ABC is given, where BCD is the exterior angle.
• \angle BAC + \angle ABC +\angle BCA = 180^0
• From the equalities, the angle \angle BCD + \angle BCA = 180^0
• We get \angle BCD = \angle BAC+\angle ABC.