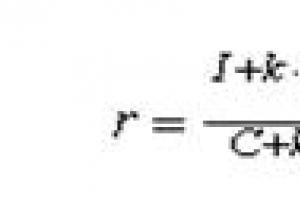Transverse bending of the rod. Clean bend Direct cross bend solution

For a cantilever beam loaded with a distributed load of intensity kN / m and a concentrated moment kN m (Fig. 3.12), it is required: to build diagrams of shear forces and bending moments, select a beam of circular cross section at an allowable normal stress kN / cm2 and check the strength of the beam according to shear stresses at permissible shear stress kN/cm2. Beam dimensions m; m; m.

Design scheme for the problem of direct transverse bending

Rice. 3.12

Solving the problem of "direct transverse bending"

Determining support reactions

The horizontal reaction in the embedment is zero, since external loads in the direction of the z-axis do not act on the beam.

We choose the directions of the remaining reactive forces that arise in the embedment: let's direct the vertical reaction, for example, down, and the moment - clockwise. Their values are determined from the equations of statics:

When compiling these equations, we consider the moment to be positive when rotating counterclockwise, and the projection of the force is positive if its direction coincides with the positive direction of the y axis.

From the first equation we find the moment in the termination:

From the second equation - vertical reaction:

The positive values obtained by us for the moment and vertical reaction in the termination indicate that we have guessed their directions.

In accordance with the nature of the fastening and loading of the beam, we divide its length into two sections. Along the boundaries of each of these sections, we outline four cross sections (see Fig. 3.12), in which we will calculate the values of shear forces and bending moments by the method of sections (ROZU).

Section 1. Let's mentally discard the right side of the beam. Let's replace its action on the remaining left side with a cutting force and a bending moment. For the convenience of calculating their values, we close the right side of the beam discarded by us with a piece of paper, aligning the left edge of the sheet with the section under consideration.

Recall that the shear force arising in any cross section must balance all external forces (active and reactive) that act on the part of the beam we are considering (that is, visible). Therefore, the shearing force must be equal to the algebraic sum of all the forces that we see.

We also give the sign rule for the shearing force: an external force acting on the considered part of the beam and tending to “rotate” this part relative to the section in a clockwise direction causes a positive shearing force in the section. Such an external force is included in the algebraic sum for the definition with a plus sign.

In our case, we see only the reaction of the support, which rotates the visible part of the beam relative to the first section (relative to the edge of the piece of paper) counterclockwise. That's why

kN.

The bending moment in any section must balance the moment created by external forces that we see with respect to the section under consideration. Therefore, it is equal to the algebraic sum of the moments of all efforts that act on the part of the beam we are considering, relative to the section under consideration (in other words, relative to the edge of the piece of paper). In this case, an external load bending the considered part of the beam with a convexity downwards causes a positive bending moment in the section. And the moment created by such a load is included in the algebraic sum for the definition with a plus sign.

We see two efforts: the reaction and the moment in termination. However, the arm of the force with respect to section 1 is equal to zero. That's why

kN m

We took the plus sign because the reactive moment bends the visible part of the beam with a convexity downwards.

Section 2. As before, we will cover the entire right side of the beam with a piece of paper. Now, unlike the first section, the force has a shoulder: m. Therefore

kN; kN m

Section 3. Closing the right side of the beam, we find

kN;

Section 4. Let's close the left side of the beam with a leaf. Then

kN m

Based on the values found, we build diagrams of shear forces (Fig. 3.12, b) and bending moments (Fig. 3.12, c).

Under unloaded sections, the diagram of shear forces runs parallel to the axis of the beam, and under a distributed load q, along an inclined straight line upwards. Under the support reaction on the diagram there is a jump down by the value of this reaction, that is, by 40 kN.

On the diagram of bending moments, we see a break under the support reaction. The fracture angle is directed towards the reaction of the support. Under a distributed load q, the diagram changes along a quadratic parabola, the convexity of which is directed towards the load. In section 6 on the diagram there is an extremum, since the diagram of the shearing force in this place passes through the zero value here.

Determine the required diameter of the cross section of the beam

The strength condition for normal stresses has the form:

where is the moment of resistance of the beam in bending. For a beam of circular cross section, it is equal to:

The bending moment with the largest absolute value occurs in the third section of the beam: kN cm

Then the required beam diameter is determined by the formula

cm.

We accept mm. Then

kN/cm2 kN/cm2.

"Overvoltage" is

what is allowed.

We check the strength of the beam for the highest tangential stresses

The highest shear stresses that occur in the cross section of a circular beam are calculated by the formula

where is the cross-sectional area.

According to the plot, the largest algebraic value of the shear force is equal to kN. Then

kN/cm2 kN/cm2,

that is, the condition of strength and shear stresses is fulfilled, moreover, with a large margin.

An example of solving the problem "direct transverse bending" No. 2

Condition of the problem example for direct transverse bending

For a hinged beam loaded with a distributed load of intensity kN / m, a concentrated force kN and a concentrated moment kN m (Fig. 3.13), it is required to plot the shear forces and bending moments and select an I-beam cross section with an allowable normal stress kN / cm2 and permissible shear stress kN/cm2. Beam span m.

An example of a task for a straight bend - a design scheme

Rice. 3.13

Solution of an example of a straight bend problem

Determining support reactions

For a given pivotally supported beam, it is necessary to find three support reactions: , and . Since only vertical loads act on the beam, perpendicular to its axis, the horizontal reaction of the fixed hinged support A is equal to zero: .

The directions of vertical reactions and are chosen arbitrarily. Let's direct, for example, both vertical reactions upwards. To calculate their values, we compose two equations of statics:

Recall that the resultant linear load, uniformly distributed over a section of length l, is equal to, that is, equal to the area of the diagram of this load and it is applied at the center of gravity of this diagram, that is, in the middle of the length.

;

kN.

We check: .

Recall that forces whose direction coincides with the positive direction of the y-axis are projected (projected) onto this axis with a plus sign:

that is correct.

We build diagrams of shear forces and bending moments

We break the length of the beam into separate sections. The boundaries of these areas are the points of application of concentrated forces (active and / or reactive), as well as points corresponding to the beginning and end of the distributed load. There are three such areas in our problem. Along the boundaries of these sections, we outline six cross sections, in which we will calculate the values of shear forces and bending moments (Fig. 3.13, a).

Section 1. Let's mentally discard the right side of the beam. For the convenience of calculating the shear force and bending moment arising in this section, we close the part of the beam discarded by us with a piece of paper, aligning the left edge of the piece of paper with the section itself.

The shearing force in the beam section is equal to the algebraic sum of all external forces (active and reactive) that we see. In this case, we see the reaction of the support and the linear load q, distributed over an infinitely small length. The resultant linear load is zero. That's why

kN.

The plus sign is taken because the force rotates the visible part of the beam relative to the first section (the edge of the piece of paper) in a clockwise direction.

The bending moment in the section of the beam is equal to the algebraic sum of the moments of all the forces that we see, relative to the section under consideration (that is, relative to the edge of a piece of paper). We see the reaction of the support and the linear load q, distributed over an infinitely small length. However, the leverage of the force is zero. The resultant linear load is also equal to zero. That's why

Section 2. As before, we will cover the entire right side of the beam with a piece of paper. Now we see the reaction and the load q acting on a section of length . The resultant linear load is equal to . It is attached in the middle of a section with a length of . That's why

Recall that when determining the sign of the bending moment, we mentally free the part of the beam that we see from all the actual support fastenings and imagine it as if pinched in the section under consideration (that is, the left edge of the piece of paper is mentally represented by us as a rigid seal).

Section 3. Let's close the right part. Get

Section 4. We close the right side of the beam with a leaf. Then

Now, to control the correctness of the calculations, let's cover the left side of the beam with a piece of paper. We see the concentrated force P, the reaction of the right support and the linear load q, distributed over an infinitely small length. The resultant linear load is zero. That's why

kN m

That is, everything is correct.

Section 5. Still close the left side of the beam. Will have

kN;

kN m

Section 6. Let's close the left side of the beam again. Get

kN;

Based on the values found, we build diagrams of shear forces (Fig. 3.13, b) and bending moments (Fig. 3.13, c).

We are convinced that under the unloaded section the diagram of the shear forces runs parallel to the axis of the beam, and under a distributed load q - along a straight line with a downward slope. There are three jumps on the diagram: under the reaction - up by 37.5 kN, under the reaction - up by 132.5 kN and under the force P - down by 50 kN.

On the diagram of bending moments, we see breaks under the concentrated force P and under the support reactions. The fracture angles are directed towards these forces. Under a distributed load of intensity q, the diagram changes along a quadratic parabola, the convexity of which is directed towards the load. Under the concentrated moment there is a jump of 60 kN m, that is, by the magnitude of the moment itself. In section 7 on the diagram there is an extremum, since the diagram of the shear force for this section passes through the zero value (). Let us determine the distance from section 7 to the left support.

Straight bend. Flat transverse bend Plotting diagrams of internal force factors for beams Plotting Q and M diagrams using equations Plotting Q and M diagrams using characteristic sections (points) Calculations for strength at straight bend beams Principal stresses in bending. Complete verification of the strength of beams Understanding the center of bending Determination of displacements in beams during bending. Concepts of deformation of beams and conditions of their rigidity Differential equation of the bent axis of the beam Method of direct integration Examples of determining displacements in beams by the method of direct integration Physical meaning of the constants of integration Method of initial parameters (universal equation of the bent axis of the beam). Examples of determining displacements in a beam using the method of initial parameters Determination of displacements using the Mohr method. A.K.'s rule Vereshchagin. Calculation of the Mohr integral according to A.K. Vereshchagin Examples of determination of displacements by means of Mohr's integral Bibliography Direct bending. Flat transverse bend. 1.1. Plotting diagrams of internal force factors for beams Direct bending is a type of deformation in which two internal force factors arise in the cross sections of the bar: a bending moment and a transverse force. In a particular case, the transverse force can be equal to zero, then the bend is called pure. With a flat transverse bending, all forces are located in one of the main planes of inertia of the rod and are perpendicular to its longitudinal axis, the moments are located in the same plane (Fig. 1.1, a, b). Rice. 1.1 The transverse force in an arbitrary cross section of the beam is numerically equal to the algebraic sum of the projections onto the normal to the axis of the beam of all external forces acting on one side of the section under consideration. Shear force in section m-n beams (Fig. 1.2, a) is considered positive if the resultant of external forces to the left of the section is directed upwards, and to the right - downwards, and negative - in the opposite case (Fig. 1.2, b). Rice. 1.2 When calculating the transverse force in a given section, the external forces lying to the left of the section are taken with a plus sign if they are directed upwards, and with a minus sign if downwards. For the right side of the beam - vice versa. 5 The bending moment in an arbitrary cross section of the beam is numerically equal to the algebraic sum of the moments about the central axis z of the section of all external forces acting on one side of the section under consideration. The bending moment in the m-n section of the beam (Fig. 1.3, a) is considered positive if the resultant moment of external forces is directed clockwise from the section to the left of the section, and counterclockwise to the right, and negative - in the opposite case (Fig. 1.3, b). Rice. 1.3 When calculating the bending moment in a given section, the moments of external forces lying to the left of the section are considered positive if they are directed clockwise. For the right side of the beam - vice versa. It is convenient to determine the sign of the bending moment by the nature of the deformation of the beam. The bending moment is considered positive if, in the section under consideration, the cut-off part of the beam bends with a convexity downward, i.e., the lower fibers are stretched. Otherwise, the bending moment in the section is negative. Between the bending moment M, the transverse force Q and the intensity of the load q, there are differential dependencies. 1. The first derivative of the transverse force along the abscissa of the section is equal to the intensity of the distributed load, i.e. . (1.1) 2. The first derivative of the bending moment along the abscissa of the section is equal to the transverse force, i.e. . (1.2) 3. The second derivative with respect to the abscissa of the section is equal to the intensity of the distributed load, i.e. . (1.3) We consider the distributed load directed upwards to be positive. A number of important conclusions follow from the differential dependencies between M, Q, q: 1. If on the beam section: a) the transverse force is positive, then the bending moment increases; b) the transverse force is negative, then the bending moment decreases; c) the transverse force is zero, then the bending moment has a constant value (pure bending); 6 d) the transverse force passes through zero, changing sign from plus to minus, max M M, otherwise M Mmin. 2. If there is no distributed load on the beam section, then the transverse force is constant, and the bending moment changes linearly. 3. If there is a uniformly distributed load on the section of the beam, then the transverse force changes according to a linear law, and the bending moment - according to the law of a square parabola, convex in the direction of the load (in the case of plotting M from the side of the stretched fibers). 4. In the section under the concentrated force, the diagram Q has a jump (by the magnitude of the force), the diagram M has a break in the direction of the force. 5. In the section where a concentrated moment is applied, the diagram M has a jump equal to the value of this moment. This is not reflected in the Q plot. Under complex loading, beams build diagrams of transverse forces Q and bending moments M. Plot Q (M) is a graph showing the law of change in the transverse force (bending moment) along the length of the beam. Based on the analysis of diagrams M and Q, dangerous sections of the beam are established. The positive ordinates of the Q diagram are plotted upwards, and the negative ordinates are plotted downwards from the base line drawn parallel to the longitudinal axis of the beam. The positive ordinates of the diagram M are laid down, and the negative ordinates are plotted upwards, i.e., the diagram M is built from the side of the stretched fibers. The construction of diagrams Q and M for beams should begin with the definition of support reactions. For a beam with one fixed end and the other free end, plotting Q and M can be started from the free end without defining reactions in the embedment. 1.2. The construction of diagrams Q and M according to the Balk equations is divided into sections, within which the functions for the bending moment and the shear force remain constant (have no discontinuities). The boundaries of the sections are the points of application of concentrated forces, pairs of forces and places of change in the intensity of the distributed load. On each section, an arbitrary section is taken at a distance x from the origin, and equations for Q and M are drawn up for this section. Plots Q and M are built using these equations. Example 1.1 Construct plots of shear forces Q and bending moments M for a given beam (Fig. 1.4a). Solution: 1. Determination of reactions of supports. We compose the equilibrium equations: from which we obtain The reactions of the supports are defined correctly. The beam has four sections Fig. 1.4 loadings: CA, AD, DB, BE. 2. Plotting Q. Plot SA. On section CA 1, we draw an arbitrary section 1-1 at a distance x1 from the left end of the beam. We define Q as the algebraic sum of all external forces acting to the left of the section 1-1: The minus sign is taken because the force acting to the left of the section is directed downward. The expression for Q does not depend on the variable x1. Plot Q in this section will be depicted as a straight line parallel to the x-axis. Plot AD. On the site, we draw an arbitrary section 2-2 at a distance x2 from the left end of the beam. We define Q2 as the algebraic sum of all external forces acting to the left of section 2-2: 8 The value of Q is constant on the section (does not depend on the variable x2). Plot Q on the plot is a straight line parallel to the x-axis. DB site. On the site, we draw an arbitrary section 3-3 at a distance x3 from the right end of the beam. We define Q3 as the algebraic sum of all external forces acting to the right of section 3-3: The resulting expression is the equation of an inclined straight line. Plot B.E. On the site, we draw a section 4-4 at a distance x4 from the right end of the beam. We define Q as the algebraic sum of all external forces acting to the right of section 4-4: 4 Here, the plus sign is taken because the resultant load to the right of section 4-4 is directed downward. Based on the obtained values, we build diagrams Q (Fig. 1.4, b). 3. Plotting M. Plot m1. We define the bending moment in section 1-1 as the algebraic sum of the moments of forces acting to the left of section 1-1. is the equation of a straight line. Section A 3 Define the bending moment in section 2-2 as the algebraic sum of the moments of forces acting to the left of section 2-2. is the equation of a straight line. Plot DB 4 We define the bending moment in section 3-3 as the algebraic sum of the moments of forces acting to the right of section 3-3. is the equation of a square parabola. 9 Find three values at the ends of the section and at the point with coordinate xk , where Section BE 1 Define the bending moment in section 4-4 as the algebraic sum of the moments of forces acting to the right of section 4-4. - the equation of a square parabola we find three values of M4: Based on the obtained values, we build a plot M (Fig. 1.4, c). In sections CA and AD, plot Q is limited by straight lines parallel to the abscissa axis, and in sections DB and BE, by oblique straight lines. In the sections C, A and B on the diagram Q there are jumps by the magnitude of the corresponding forces, which serves as a check of the correctness of the construction of the diagram Q. In sections where Q  0, the moments increase from left to right. In sections where Q  0, the moments decrease. Under the concentrated forces there are kinks in the direction of the action of the forces. Under the concentrated moment, there is a jump by the moment value. This indicates the correctness of plotting M. Example 1.2 Construct plots Q and M for a beam on two supports, loaded with a distributed load, the intensity of which varies linearly (Fig. 1.5, a). Solution Determination of support reactions. The resultant of the distributed load is equal to the area of the triangle representing the load diagram and is applied at the center of gravity of this triangle. We make up the sums of the moments of all forces relative to points A and B: Plotting Q. Let's draw an arbitrary section at a distance x from the left support. The ordinate of the load diagram corresponding to the section is determined from the similarity of triangles The resultant of that part of the load that is located to the left of the section The shear force in the section is equal to zero: Plot Q is shown in fig. 1.5, b. The bending moment in an arbitrary section is equal to The bending moment changes according to the law of a cubic parabola: The maximum value of the bending moment is in the section, where 0, i.e. at. 1.5, c. 1.3. Construction of diagrams Q and M by characteristic sections (points) Using the differential relationships between M, Q, q and the conclusions arising from them, it is advisable to build diagrams Q and M by characteristic sections (without formulating equations). Using this method, the values of Q and M are calculated in characteristic sections. The characteristic sections are the boundary sections of the sections, as well as the sections where the given internal force factor has an extreme value. Within the limits between the characteristic sections, the outline 12 of the diagram is established on the basis of differential dependencies between M, Q, q and the conclusions arising from them. Example 1.3 Construct diagrams Q and M for the beam shown in fig. 1.6, a. Rice. 1.6. Solution: We start plotting Q and M diagrams from the free end of the beam, while the reactions in the embedment can be omitted. The beam has three loading areas: AB, BC, CD. There is no distributed load in sections AB and BC. The transverse forces are constant. Plot Q is limited by straight lines parallel to the x-axis. Bending moments change linearly. Plot M is limited to straight lines inclined to the x-axis. On section CD there is a uniformly distributed load. The transverse forces change linearly, and the bending moments change according to the law of a square parabola with a convexity in the direction of the distributed load. At the boundary of sections AB and BC, the transverse force changes abruptly. At the boundary of sections BC and CD, the bending moment changes abruptly. 1. Plotting Q. We calculate the values of transverse forces Q in the boundary sections of the sections: Based on the results of calculations, we build a diagram Q for the beam (Fig. 1, b). It follows from the diagram Q that the transverse force in the section CD is equal to zero in the section spaced at a distance qa a q from the beginning of this section. In this section, the bending moment has a maximum value. 2. Construction of diagram M. We calculate the values of bending moments in the boundary sections of the sections: Example 1.4 According to the given diagram of bending moments (Fig. 1.7, a) for the beam (Fig. 1.7, b), determine the acting loads and plot Q. The circle indicates the vertex of the square parabola. Solution: Determine the loads acting on the beam. Section AC is loaded with a uniformly distributed load, since the diagram M in this section is a square parabola. In the reference section B, a concentrated moment is applied to the beam, acting in a clockwise direction, since on the diagram M we have an upward jump by the magnitude of the moment. In the NE section, the beam is not loaded, since the diagram M in this section is limited by an inclined straight line. The reaction of support B is determined from the condition that the bending moment in section C is equal to zero, i.e. To determine the intensity of the distributed load, we compose an expression for the bending moment in section A as the sum of the moments of forces on the right and equate to zero. Now we determine the reaction of support A. To do this we will compose an expression for bending moments in the section as the sum of the moments of forces on the left. The calculation scheme of a beam with a load is shown in fig. 1.7, c. Starting from the left end of the beam, we calculate the values of the transverse forces in the boundary sections of the sections: Plot Q is shown in fig. 1.7, d. The considered problem can be solved by compiling functional dependencies for M, Q in each section. Let's choose the origin of coordinates at the left end of the beam. On the section AC, the plot M is expressed by a square parabola, the equation of which is of the form Constants a, b, c, we find from the condition that the parabola passes through three points with known coordinates: Substituting the coordinates of the points into the equation of the parabola, we get: The expression for the bending moment will be , we obtain the dependence for the transverse force After differentiating the function Q, we obtain an expression for the intensity of the distributed load In the section NE, the expression for the bending moment is represented as a linear function To determine the constants a and b, we use the conditions that this line passes through two points whose coordinates are known We obtain two equations: ,b of which we have a 20. The equation for the bending moment in the section NE will be After a twofold differentiation of M2, we will find. Based on the found values of M and Q, we build diagrams of bending moments and shear forces for the beam. In addition to the distributed load, concentrated forces are applied to the beam in three sections, where there are jumps on the Q diagram, and concentrated moments in the section where there is a jump on the M diagram. Example 1.5 For a beam (Fig. 1.8, a), determine the rational position of the hinge C, at which the largest bending moment in the span is equal to the bending moment in the embedment (in absolute value). Build diagrams Q and M. Solution Determination of reactions of supports. Despite the fact that the total number of support links is four, the beam is statically determinate. The bending moment in hinge C is equal to zero, which allows us to make an additional equation: the sum of the moments about the hinge of all external forces acting on one side of this hinge is equal to zero. Compose the sum of the moments of all forces to the right of the hinge C. Diagram Q for the beam is limited by an inclined straight line, since q = const. We determine the values of transverse forces in the boundary sections of the beam: The abscissa xK of the section, where Q = 0, is determined from the equation whence Plot M for the beam is limited by a square parabola. Expressions for bending moments in sections, where Q = 0, and in the embedment are written respectively as follows: From the condition of equality of moments, we obtain a quadratic equation with respect to the desired parameter x: Real value x2x 1.029 m. in the characteristic sections of the beam Figure 1.8, b shows the diagram Q, and in Figure. 1.8, c - plot M. The considered problem could be solved by dividing the hinged beam into its constituent elements, as shown in fig. 1.8, d. At the beginning, the reactions of the supports VC and VB are determined. Plots Q and M are constructed for the suspension beam SV from the action of the load applied to it. Then they move to the main beam AC, loading it with an additional force VC, which is the pressure force of the beam CB on the beam AC. After that, diagrams Q and M are built for the AC beam. 1.4. Strength calculations for direct bending of beams Strength calculation for normal and shear stresses. With a direct bending of a beam, normal and shear stresses arise in its cross sections (Fig. 1.9). 18 Fig. 1.9 Normal stresses are related to the bending moment, shear stresses are related to the transverse force. In direct pure bending, shear stresses are equal to zero. Normal stresses at an arbitrary point of the beam cross section are determined by the formula (1.4) where M is the bending moment in the given section; Iz is the moment of inertia of the section relative to the neutral axis z; y is the distance from the point where the normal stress is determined to the neutral z axis. Normal stresses along the height of the section change linearly and reach the greatest value at the points most distant from the neutral axis If the section is symmetrical about the neutral axis (Fig. 1.11), then Fig. 1.11 the greatest tensile and compressive stresses are the same and are determined by the formula,  - axial moment of section resistance in bending. For a rectangular section with a width b and a height h: (1.7) For a circular section with a diameter d: (1.8) For an annular section   are the inner and outer diameters of the ring, respectively. For beams made of plastic materials, the most rational are symmetrical 20 section shapes (I-beam, box-shaped, annular). For beams made of brittle materials that do not equally resist tension and compression, sections that are asymmetrical about the neutral axis z (ta-br., U-shaped, asymmetrical I-beam) are rational. For beams of constant section made of plastic materials with symmetrical section shapes, the strength condition is written as follows: (1.10) where Mmax is the maximum bending moment modulo; - allowable stress for the material. For beams of constant section made of ductile materials with asymmetric cross-sectional shapes, the strength condition is written in the following form: (1.11) strength conditions - distances from the neutral axis to the most remote points of the stretched and compressed zones of the dangerous section, respectively; P - allowable stresses, respectively, in tension and compression. Fig.1.12. 21 If the bending moment diagram has sections of different signs (Fig. 1.13), then in addition to checking the section 1-1, where Mmax acts, it is necessary to calculate the maximum tensile stresses for the section 2-2 (with the largest moment of the opposite sign). Rice. 1.13 Along with the basic calculation for normal stresses, in some cases it is necessary to check the beam strength for shear stresses. Shear stresses in beams are calculated by the formula of D. I. Zhuravsky (1.13) where Q is the transverse force in the considered cross section of the beam; Szots is the static moment about the neutral axis of the area of the part of the section located on one side of the straight line drawn through the given point and parallel to the z axis; b is the width of the section at the level of the considered point; Iz is the moment of inertia of the entire section about the neutral axis z. In many cases, the maximum shear stresses occur at the level of the neutral layer of the beam (rectangle, I-beam, circle). In such cases, the shear stress strength condition is written as, (1. 14) where Qmax is the transverse force with the highest modulus; - allowable shear stress for the material. For a rectangular beam section, the strength condition has the form (1.15) A is the cross-sectional area of the beam. For a circular section, the strength condition is represented as (1.16) For an I-section, the strength condition is written as follows: (1.17) d is the wall thickness of the I-beam. Usually, the dimensions of the cross section of the beam are determined from the condition of strength for normal stresses. Checking the strength of beams for shear stresses is mandatory for short beams and beams of any length, if there are concentrated forces of large magnitude near the supports, as well as for wooden, riveted and welded beams. Example 1.6 Check the strength of a box-section beam (Fig. 1.14) for normal and shear stresses, if MPa. Build diagrams in the dangerous section of the beam. Rice. 1.14 Decision 23 1. Plot Q and M plots from characteristic sections. Considering the left side of the beam, we obtain. The diagram of the transverse forces is shown in fig. 1.14, c. The plot of bending moments is shown in fig. 5.14, g. 2. Geometric characteristics of the cross section 3. The highest normal stresses in the section C, where Mmax acts (modulo): MPa. The maximum normal stresses in the beam are practically equal to the allowable ones. 4. The greatest tangential stresses in section C (or A), where max Q acts (modulo): Here is the static moment of the half-section area relative to the neutral axis; b2 cm is the width of the section at the level of the neutral axis. Fig. 5. Tangential stresses at a point (in the wall) in section C: Fig. 1.15 Here Szomc 834.5 108 cm3 is the static moment of the area of the part of the section located above the line passing through the point K1; b2 cm is the wall thickness at the level of point K1. Plots  and  for section C of the beam are shown in fig. 1.15. Example 1.7 For the beam shown in fig. 1.16, a, it is required: 1. Construct diagrams of transverse forces and bending moments along characteristic sections (points). 2. Determine the dimensions of the cross section in the form of a circle, rectangle and I-beam from the condition of strength for normal stresses, compare the cross-sectional areas. 3. Check the selected dimensions of the beam sections for shear stresses. Given: Solution: 1. Determine the reactions of the beam supports Check: 2. Plot Q and M diagrams. Values of transverse forces in characteristic sections of the beam 25 Fig. 1.16 In sections CA and AD, the load intensity q = const. Therefore, in these sections, the diagram Q is limited to straight lines inclined to the axis. In the section DB, the intensity of the distributed load q \u003d 0, therefore, in this section, the diagram Q is limited to a straight line parallel to the x axis. Diagram Q for the beam is shown in fig. 1.16b. Values of bending moments in the characteristic sections of the beam: In the second section, we determine the abscissa x2 of the section, in which Q = 0: The maximum moment in the second section Diagram M for the beam is shown in fig. 1.16, c. 2. We compose the strength condition for normal stresses from which we determine the required axial section modulus from the expression determined the required diameter d of a circular section beam Circular section area For a rectangular beam Required section height Rectangular section area According to the tables of GOST 8239-89, we find the nearest greater value of the axial moment of resistance 597 cm3, which corresponds to the I-beam No. 33 with the characteristics: A z 9840 cm4. Tolerance check: (underload by 1% of the allowable 5%) the nearest I-beam No. 30 (W 2 cm3) leads to a significant overload (more than 5%). We finally accept the I-beam No. 33. We compare the areas of circular and rectangular sections with the smallest area A of the I-beam: Of the three considered sections, the I-section is the most economical. 3. We calculate the largest normal stresses in the dangerous section 27 of the I-beam (Fig. 1.17, a): Normal stresses in the wall near the flange of the I-section of the beam Diagram normal stresses in the dangerous section of the beam is shown in fig. 1.17b. 5. We determine the largest shear stresses for the selected sections of the beam. a) rectangular section of the beam: b) round section beams: c) I-beam section: Shear stresses in the wall near the flange of the I-beam in the dangerous section A (on the right) (at point 2): The diagram of shear stresses in the dangerous sections of the I-beam is shown in fig. 1.17, in. The maximum shear stresses in the beam do not exceed the allowable stresses Example 1.8 Determine the allowable load on the beam (Fig. 1.18, a), if 60MPa, the cross-sectional dimensions are given (Fig. 1.19, a). Construct a diagram of normal stresses in the dangerous section of the beam under the allowable load. Fig 1.18 1. Determination of the reactions of the beam supports. In view of the symmetry of the system 2. Construction of diagrams Q and M from characteristic sections. Shear forces in the characteristic sections of the beam: Diagram Q for the beam is shown in fig. 5.18b. Bending moments in the characteristic sections of the beam For the second half of the beam, the ordinates M are along the axes of symmetry. Diagram M for the beam is shown in fig. 1.18b. 3. Geometric characteristics of the section (Fig. 1.19). We divide the figure into two simple elements: an I-beam - 1 and a rectangle - 2. Fig. 1.19 According to the assortment for I-beam No. 20, we have For a rectangle: Static moment of the sectional area relative to the z1 axis Distance from the z1 axis to the center of gravity of the section Moment of inertia of the section relative to the main central axis z of the entire section according to the formulas for the transition to parallel axes dangerous point "a" (Fig. 1.19) in the dangerous section I (Fig. 1.18): After substituting numerical data 5. With a permissible load in the dangerous section, the normal stresses at points "a" and "b" will be equal: dangerous section 1-1 is shown in fig. 1.19b.

10.1. General concepts and definitions

bend- this is a type of loading in which the rod is loaded with moments in planes passing through the longitudinal axis of the rod.

A rod that works in bending is called a beam (or bar). In the future, we will consider straight beams, the cross section of which has at least one axis of symmetry.

In the resistance of materials, bending is flat, oblique and complex.

flat bend- bending, in which all the forces bending the beam lie in one of the planes of symmetry of the beam (in one of the main planes).

The main planes of inertia of the beam are the planes passing through the main axes of the cross sections and the geometric axis of the beam (x axis).

oblique bend- bending, in which the loads act in one plane that does not coincide with the main planes of inertia.

Complex bend- bending, in which the loads act in different (arbitrary) planes.

10.2. Determination of internal bending forces

Let us consider two characteristic cases of bending: in the first case, the cantilever beam is bent by the concentrated moment Mo; in the second, by the concentrated force F.

Using the method of mental sections and compiling the equilibrium equations for the cut-off parts of the beam, we determine the internal forces in both cases:

The rest of the equilibrium equations are obviously identically equal to zero.

Thus, in the general case of flat bending in the beam section, out of six internal forces, two arise - bending moment Mz and shear force Qy (or when bending about another main axis - the bending moment My and the transverse force Qz).

In this case, in accordance with the two considered cases of loading, flat bending can be divided into pure and transverse.

Pure bend- flat bending, in which only one out of six internal forces arises in the sections of the rod - a bending moment (see the first case).

transverse bend- bending, in which, in addition to the internal bending moment, a transverse force also arises in the sections of the rod (see the second case).

Strictly speaking, to simple species resistance applies only to pure bending; transverse bending is conditionally referred to as simple types of resistance, since in most cases (for sufficiently long beams) the action of a transverse force can be neglected in strength calculations.

When determining internal forces, we will adhere to the following rule of signs:

1) the transverse force Qy is considered positive if it tends to rotate the beam element under consideration clockwise;

2) the bending moment Mz is considered positive if, when the beam element is bent, the upper fibers of the element are compressed, and the lower fibers are stretched (umbrella rule).

Thus, the solution of the problem of determining the internal forces during bending will be built according to the following plan: 1) at the first stage, considering the equilibrium conditions of the structure as a whole, we determine, if necessary, the unknown reactions of the supports (note that for a cantilever beam, reactions in the embedment can be and not found if we consider the beam from the free end); 2) at the second stage, we select the characteristic sections of the beam, taking as the boundaries of the sections the points of application of forces, points of change in the shape or dimensions of the beam, points of fastening of the beam; 3) at the third stage, we determine the internal forces in the beam sections, considering the equilibrium conditions for the beam elements in each of the sections.

10.3. Differential dependencies in bending

Let us establish some relationships between internal forces and external loads in bending, as well as characteristics diagrams Q and M, the knowledge of which will facilitate the construction of diagrams and allow you to control their correctness. For convenience of notation, we will denote: M≡Mz, Q≡Qy.

Let's allocate a small element dx in a section of a beam with an arbitrary load in a place where there are no concentrated forces and moments. Since the entire beam is in equilibrium, the element dx will also be in equilibrium under the action of transverse forces applied to it, bending moments and external load. Since Q and M generally vary along

axis of the beam, then in the sections of the element dx there will be transverse forces Q and Q + dQ, as well as bending moments M and M + dM. From the equilibrium condition of the selected element, we obtain

The first of the two written equations gives the condition

From the second equation, neglecting the term q dx (dx/2) as an infinitesimal quantity of the second order, we find

Considering expressions (10.1) and (10.2) together we can get

Relations (10.1), (10.2) and (10.3) are called differential dependences of D. I. Zhuravsky in bending.

The analysis of the above differential dependencies in bending allows us to establish some features (rules) for constructing diagrams of bending moments and shear forces: a - in areas where there is no distributed load q, diagrams Q are limited to straight lines parallel to the base, and diagrams M are inclined straight lines; b - in sections where a distributed load q is applied to the beam, the Q diagrams are limited by inclined straight lines, and the M diagrams are limited by quadratic parabolas.

In this case, if we build the diagram M “on a stretched fiber”, then the convexity of the parabola will be directed in the direction of action of q, and the extremum will be located in the section where the diagram Q intersects the base line; c - in sections where a concentrated force is applied to the beam, on the Q diagram there will be jumps by the value and in the direction of this force, and on the M diagram there are kinks, the tip directed in the direction of this force; d - in sections where a concentrated moment is applied to the beam, there will be no changes on the Q diagram, and on the M diagram there will be jumps by the value of this moment; e - in sections where Q>0, the moment M increases, and in sections where Q<0, момент М убывает (см. рисунки а–г).

10.4. Normal stresses in pure bending of a straight beam

Let us consider the case of a pure planar bending of a beam and derive a formula for determining the normal stresses for this case.

Note that in the theory of elasticity it is possible to obtain an exact dependence for normal stresses in pure bending, but if to solve this problem by methods of resistance of materials, it is necessary to introduce some assumptions.

There are three such hypotheses for bending:

a - the hypothesis of flat sections (Bernoulli's hypothesis) - the sections are flat before deformation and remain flat after deformation, but only rotate about a certain line, which is called the neutral axis of the beam section. In this case, the fibers of the beam, lying on one side of the neutral axis, will be stretched, and on the other, compressed; fibers lying on the neutral axis do not change their length;

b - the hypothesis of the constancy of normal stresses - stresses acting at the same distance y from the neutral axis are constant across the width of the beam;

c – hypothesis about the absence of lateral pressures – neighboring longitudinal fibers do not press on each other.

The static side of the problem

To determine the stresses in the cross sections of the beam, we consider, first of all, the static sides of the problem. Applying the method of mental sections and compiling the equilibrium equations for the cut-off part of the beam, we find the internal forces during bending. As shown earlier, the only internal force acting in the section of the bar in pure bending is the internal bending moment, which means that normal stresses associated with it will arise here.

We find the relationship between internal forces and normal stresses in the beam section by considering the stresses on the elementary area dA, selected in the cross section A of the beam at a point with coordinates y and z (the y axis is directed downwards for ease of analysis):

As we can see, the problem is internally statically indeterminate, since the nature of the distribution of normal stresses over the cross section is unknown. To solve the problem, consider the geometric pattern of deformations.

The geometric side of the problem

Consider the deformation of a beam element of length dx selected from a bending rod at an arbitrary point with coordinate x. Taking into account the previously accepted hypothesis of flat sections, after bending the beam section, turn relative to the neutral axis (n.r.) by an angle dϕ, while the fiber ab, which is at a distance y from the neutral axis, will turn into a circular arc a1b1, and its length will change by some size. Here we recall that the length of the fibers lying on the neutral axis does not change, and therefore the arc a0b0 (the radius of curvature of which we denote by ρ) has the same length as the segment a0b0 before deformation a0b0=dx.

Let us find the relative linear deformation εx of the fiber ab of the curved beam.

straight bend- this is a type of deformation in which two internal force factors arise in the cross sections of the rod: a bending moment and a transverse force.

Pure bend- this is a special case of direct bending, in which only a bending moment occurs in the cross sections of the rod, and the transverse force is zero.

Pure Bend Example - Plot CD on the rod AB. Bending moment is the value Pa pair of external forces causing bending. From the equilibrium of the part of the rod to the left of the cross section mn it follows that the internal forces distributed over this section are statically equivalent to the moment M, equal and opposite to the bending moment Pa.

To find the distribution of these internal forces over the cross section, it is necessary to consider the deformation of the bar.

In the simplest case, the rod has a longitudinal plane of symmetry and is subjected to the action of external bending pairs of forces located in this plane. Then the bend will occur in the same plane.

rod axis nn 1 is a line passing through the centers of gravity of its cross sections.

Let the cross section of the rod be a rectangle. Draw two vertical lines on its faces mm And pp. When bent, these lines remain straight and rotate so that they remain perpendicular to the longitudinal fibers of the rod.

A further theory of bending is based on the assumption that not only lines mm And pp, but the entire flat cross section of the rod remains flat after bending and normal to the longitudinal fibers of the rod. Therefore, when bending, the cross sections mm And pp rotate relative to each other around axes perpendicular to the bending plane (drawing plane). In this case, the longitudinal fibers on the convex side experience tension, and the fibers on the concave side experience compression.

neutral surface is a surface that does not experience deformation during bending. (Now it is located perpendicular to the drawing, the deformed axis of the rod nn 1 belongs to this surface).

Neutral sectional axis- this is the intersection of a neutral surface with any with any cross section (now also located perpendicular to the drawing).

Let an arbitrary fiber be at a distance y from a neutral surface. ρ is the radius of curvature of the curved axis. Dot O is the center of curvature. Let's draw a line n 1 s 1 parallel mm.ss 1 is the absolute elongation of the fiber.

Relative extension ε x fibers

It follows that deformation of the longitudinal fibers proportional to distance y from the neutral surface and inversely proportional to the radius of curvature ρ .

Longitudinal elongation of the fibers of the convex side of the rod is accompanied by lateral constriction, and the longitudinal shortening of the concave side - lateral extension, as in the case of simple stretching and contraction. Because of this, the appearance of all cross sections changes, the vertical sides of the rectangle become slanted. Lateral deformation z:

μ - Poisson's ratio.

As a result of this distortion, all straight cross-sectional lines parallel to the axis z, are bent so as to remain normal to the sides of the section. The radius of curvature of this curve R will be more than ρ in the same way as ε x is greater in absolute value than ε z , and we get

These deformations of the longitudinal fibers correspond to stresses

The voltage in any fiber is proportional to its distance from the neutral axis. n 1 n 2. Position of the neutral axis and radius of curvature ρ are two unknowns in the equation for σ x - can be determined from the condition that the forces distributed over any cross section form a pair of forces that balances the external moment M.

All of the above is also true if the rod does not have a longitudinal plane of symmetry in which the bending moment acts, so long as the bending moment acts in the axial plane, which contains one of the two main axes cross section. These planes are called main bending planes.

When there is a plane of symmetry and the bending moment acts in this plane, the deflection occurs in it. Moments of internal forces about the axis z balance the external moment M. Moments of effort relative to the axis y are mutually destroyed.

bend called deformation, in which the axis of the rod and all its fibers, i.e., longitudinal lines parallel to the axis of the rod, are bent under the action of external forces. The simplest case of bending is obtained when the external forces lie in a plane passing through the central axis of the rod and do not project onto this axis. Such a case of bending is called transverse bending. Distinguish flat bend and oblique.

flat bend- such a case when the bent axis of the rod is located in the same plane in which external forces act.

Oblique (complex) bend- such a case of bending, when the bent axis of the rod does not lie in the plane of action of external forces.

A bending bar is commonly referred to as beam.

With a flat transverse bending of beams in a section with a coordinate system y0x, two internal forces can occur - a transverse force Q y and a bending moment M x; in what follows, we introduce the notation Q And M. If there is no transverse force in the section or section of the beam (Q = 0), and the bending moment is not equal to zero or M is const, then such a bend is commonly called clean.

Shear force in any section of the beam is numerically equal to the algebraic sum of the projections onto the axis of all forces (including support reactions) located on one side (any) of the section.

Bending moment in the beam section is numerically equal to the algebraic sum of the moments of all forces (including support reactions) located on one side (any) of the section drawn relative to the center of gravity of this section, more precisely, relative to the axis passing perpendicular to the plane of the drawing through the center of gravity of the section drawn.

Q-force is resultant distributed over the cross section of internal shear stresses, A moment M– sum of moments around the central axis of the section X internal normal stresses.

There is a differential relationship between internal forces

which is used in the construction and verification of diagrams Q and M.

Since some of the fibers of the beam are stretched, and some are compressed, and the transition from tension to compression occurs smoothly, without jumps, in the middle part of the beam there is a layer whose fibers only bend, but do not experience either tension or compression. Such a layer is called neutral layer. The line along which the neutral layer intersects with the cross section of the beam is called neutral line th or neutral axis sections. Neutral lines are strung on the axis of the beam.

Lines drawn on the side surface of the beam perpendicular to the axis remain flat when bent. These experimental data make it possible to base the conclusions of the formulas on the hypothesis of flat sections. According to this hypothesis, the sections of the beam are flat and perpendicular to its axis before bending, remain flat and become perpendicular to the bent axis of the beam when it is bent. The cross section of the beam is distorted during bending. Due to transverse deformation, the dimensions of the cross section in the compressed zone of the beam increase, and in the tension zone they are compressed.

Assumptions for deriving formulas. Normal stresses

1) The hypothesis of flat sections is fulfilled.

2) Longitudinal fibers do not press on each other and, therefore, under the action of normal stresses, linear tensions or compressions work.

3) The deformations of the fibers do not depend on their position along the width of the section. Consequently, the normal stresses, changing along the height of the section, remain the same across the width.

4) The beam has at least one plane of symmetry, and all external forces lie in this plane.

5) The material of the beam obeys Hooke's law, and the modulus of elasticity in tension and compression is the same.

6) The ratios between the dimensions of the beam are such that it works in flat bending conditions without warping or twisting.

With a pure bending of a beam on the platforms in its section, only normal stresses, determined by the formula:

where y is the coordinate of an arbitrary point of the section, measured from the neutral line - the main central axis x.

Normal bending stresses along the height of the section are distributed over linear law. On the extreme fibers, the normal stresses reach their maximum value, and in the center of gravity, the cross sections are equal to zero.

The nature of normal stress diagrams for symmetrical sections with respect to the neutral line

The nature of normal stress diagrams for sections that do not have symmetry about the neutral line

Dangerous points are those farthest from the neutral line.

Let's choose some section

For any point of the section, let's call it a point TO, the beam strength condition for normal stresses has the form:

, where i.d. - This neutral axis

This axial section modulus about the neutral axis. Its dimension is cm 3, m 3. The moment of resistance characterizes the influence of the shape and dimensions of the cross section on the magnitude of stresses.

Strength condition for normal stresses:

The normal stress is equal to the ratio of the maximum bending moment to the axial section modulus relative to the neutral axis.

If the material unequally resists stretching and compression, then two strength conditions must be used: for a stretch zone with an allowable tensile stress; for the compression zone with allowable compressive stress.

With transverse bending, the beams on the platforms in its section act as normal, and tangents voltage.